Геометрия Вселенной и главная проблема физики 3

       Главная нерешенная проблема физики,
       геометрия глобального пространства-времени               
       и основы первой космологической единой теории поля.
      

       Введение.
       Единая теория поля и главная нерешенная проблема физики.

       В настоящее время принято считать, что главной нерешенной проблемой физики является создание подтвержденной экспериментально (верифицированной) единой теории поля. Позволю себе не согласиться в этом вопросе с мнением абсолютного большинства ученых, поскольку главной загадкой всего естествознания всегда был сам факт того, что любой закон природы является одинаковым во всем пространстве и неизменным во всем времени наблюдаемой нами Вселенной. Сам этот факт давно и широко известен, и он даже стал одним из базовых принципов верификации любой теории, по крайней мере любой физической теории. Этот принцип гласит, что теория является неправильной, если приводит к выводам об изменении во времени и неодинаковости в пространстве физических законов и универсальных физических констант. Однако о причинах самого существования этого факта никто всерьез не задумывался кажется со времен древней Греции, когда великий философ Демокрит попытался впервые объяснить неизменность во времени в и одинаковость в пространстве каждого из законов природы существованием базовых материальных сущностей - фундаментальных кирпичиков всего мироздания, которые он назвал атомами. С тех пор апологеты материалистического подхода к познанию природы, к коим с необходимостью мы относим всех ученых естествоиспытателей (даже если бы они и исповедывали любую религию или идеалистическую концепцию), сильно продвинулись в плане открытия элементарных фундаментальных кирпичиков материи (например, элементарные частицы стандартной модели) и законов функционирования макро и микромира, но в философском плане решения этой главной загадки естествознания не только так и остались на уровне Демокрита, но и вообще прекратили всякие попытки решения этой загадки, ошибочно отнеся ее к неразрешимым умозрительным проблемам, лежащим в плане материализма исключительно в области непродуктивной метафизики. Но, как говорится, свято место пусто не бывает, и объективный идеализм, в форме различных религий и философских доктрин, исповедуя идею гармонии создания, как главную цель создателя, легко и непринужденно кладет в этом вопросе весь современный материализм на обе лопатки.
       У проницательного читателя естественно уже возникает вопрос: "А не может ли, единая теория поля и расширенная стандартная модель, включающая гравитон, как новый фундаментальный бозон (или может быть даже фермион), объяснить наконец эту главную загадку естествознания. Сразу же и отвечу. На мой взгляд, если фундаментальная физика в плане создания единой теории поля будет двигаться в указанном традиционном направлении, то для решения или даже для существенного продвижения к объяснению этой главной загадки я не вижу никаких оснований. Но если физикам удаться создать единую теорию поля, обосновав ее фундаментальными свойствами реальной криволинейной (по-видимому римановой), а не безосновательно постулируемой в настоящее время "плоской" (евклидовой), глобальной геометрией глобального пространства и глобального времени Вселенной, то на пути постижения главной нерешенной проблемы естествознания мы сделаем самый решительный и революционный прорыв вперед.
       Для обоснования этой гипотезы в первом приближении, я приведу следующее простейшее рассуждение. Одинаковость в пространстве и неизменность во времени всех законов физики логичнее всего (по крайней мере в терминах единой теории поля) объяснять следующим: во-первых, существует некоторое глобальное поле, то есть поле, существующее во всем пространстве и всем времени, которое имеет некие локальные и глобальные физические свойства, в том числе и нелокальные глобальные физические свойства, которые являются одинаковыми во всем пространстве и неизменными во всем времени; во-вторых, это глобальное поле, а точнее его указанные локальные и глобальные свойства, одинаковые во всем пространстве и неизменные во всем времени, полностью определяют все физические свойства всех иных полей, а также полный набор и все свойства соответствующих элементарных частиц и иных фундаментальных объектов (например, черных дыр), то есть определяют все законы физики; в-третьих, вышеперечисленных общих свойств этого глобального поля (, перечисленных в этом предложении после слов во-первых и во-вторых, ) достаточно для объяснения одинаковости в пространстве и неизменности во времени всех законов физики.
    Полагаю, что почти безальтернативно, таковым глобальным полем может быть только само глобальное пространство, существующее в глобальном времени. И хотя сам подход к пространству, в том числе и к глобальному пространству Вселенной, как физическому полю в косвенном или в прямом смысле, давно не нов, но положение о том, что геометрические свойства глобального пространства определяют все физические свойства всех иных полей, а также само использование такого подхода для решения главной нерешенной проблемы физики и естествознания является самой решительной революцией.
      
       Но совершенно очевидно, что в качестве такого глобального поля абсолютно не пригодно евклидово пространство, иначе называемое "плоским пространством", геометрию которого в настоящее время и принято считать реальной геометрией пространства Вселенной. Указанная непригодность евклидова пространства заключается в том, что оно в силу своей примитивной геометрии не может содержать достаточное количество локальных и глобальных физических свойств и соотношений этих свойств, чтобы обеспечивать и определять все наличие и многообразие свойств и физических законов наблюдаемой материи, существующей в форме различных наблюдаемых видов физических полей и соответствующих элементарных частиц.
        Ниже я обосную, что простейшей геометрией глобального пространства, которая может обеспечить минимальный набор геометрических динамических (существующих и возможно развивающихся во времени) локальных и глобальных физических свойств пространства и соотношений этих свойств, достаточный, чтобы обеспечивать и определять все наличие и многообразие физических свойств наблюдаемой материи (все законы физики), является геометрия трехмерного гипертора. Указанные соотношения таких физических свойств пространства я далее буду называть "соотношениями масштаба".
       К сожалению, в результате печально сложившегося консенсуса в настоящее время доминирует Лямбда-CDM (темная энергия (лямбда-член)- темная материя (CDM)) космологическая теория, постулирующая плоское пространство Вселенной, искусственно привлекающая необъясняемые и ненаблюдаемые темную энергию и темную материю, для объяснения движений звезд и галактик, которые не могут быть объяснены в "плоском пространстве" гравитацией наблюдаемой материи (вещества звезд, газа и черных дыр). И уж если называть вещи своими именами, то Лямбда-CDM  космологическая теория это пример, свойственного всей истории человечества и истории науки в частности, коллективного и не вполне бескорыстного заблуждения. Наиболее "серьезным" аргументом  в пользу "плоского пространства" является "наблюдаемый" якобы факт, говорящий о том, что сумма углов "глобального Вселенского треугольника", построенного с помощью наблюдения с Земли пятна флуктуации реликтового излучения, с точность до 0,1 процента равна 180 градусов. Но если расстояние (в световых годах) до этого пятна, а точнее расстояние до поверхности последнего рассеяния еще можно с некоторыми натяжками считать оцененным правильно, а угловой размер этого пятна можно считать измеренным верно, то оценка размеров этого пятна в световых годах не выдерживает уже никакой критики и кишит теми же тавтологическими приемами и теми же недоказанными допущениями, что и введение темной материи и темной энергии. По существу метод оценки размеров  пятна флуктуации реликтового излучения в световых годах уже опирается на постулат о том, что глобальное пространство Вселенной является евклидовым по крайней мере на размерах наблюдаемой Вселенной. А потому ни о какой якобы "измеренной" и составляющей 180 градусов сумме углов "глобального Вселенского треугольника" не может быть и речи. Кроме того, существует закрытое  риманово пространство, обладающее глобальной кривизной, но сохраняющее, так же как и поверхность двумерного цилиндра, сумму углов треугольника равной 180 градусов. Это пространство трехмерного тора Клиффорда (T3-R6) - трехмерного тора свободно вписанного в шестимерное евклидово пространство. В аналитической геометрии и топологии  трехмерный тор Клиффорда (T3-R6) часто называют также кубическим тором. (К сожалению в космической топологии кубическим тором часто ошибочно называют обычный трехмерный гипертор (трехмерный тор T3-R4) свободно вписанный в четырехмерное евклидово пространство, когда рассматривают его в качестве фундаментальной кубической (в общем случае параллелепипедной) ячейки универсального накрывающего пространства в виде разбитого на такие же ячейки евклидова трехмерного пространства. Эта ошибка и вытекающая из нее путаница не редко приводит авторов к ошибочным расчетам или оценкам.) В конце концов нашу Вселенную можно гипотетически представить в виде не только бесконечно малой части бесконечного открытого евклидова пространства, но и в виде достаточно малой части огромного риманова пространства (например трехмерной гиперсферы или трехмерного гипертора); в этих (последних) случаях, даже если сумма углов "глобального Вселенского треугольника" и иных наблюдаемых во Вселенной (Вселенной Большого взрыва) больших треугольников действительно окажется очень близка к 180 градусам, этот факт легко будет объяснить достаточной малостью радиуса наблюдаемой Вселенной (материи образовавшейся в результате Большого взрыва), по сравнением с размерами и радиусом (радиусами) глобального риманова пространства, (в котором наблюдаемая Вселенная (Вселенная Большого взрыва) занимает лишь небольшую часть).
        Отказ же от плоского пространства в пользу  риманова глобального пространства (например, пространства трехмерной гиперсферы или трехмерного гипертора) сразу же позволяет отказаться от темной энергии, поскольку необходимой для постоянного поддержания расширения Вселенной энергией обладает само это пространство, в силу постоянного наличия у него глобальной кривизны. В отличие от "плоского пространства", в случае риманова глобального пространства для объяснения ряда вихревых движений групп звезд в галактиках (средне и дальне отдаленные звезды) и групп галактик в скоплениях также нет прямой необходимости прибегать к помощи ненаблюдаемой темной материи, поскольку в римановом пространстве такие вихревые движения легко объяснить наличием целого ряда глобальных и локальных вихрей самого глобального пространства.
       Также ниже я покажу, что весьма вероятно, что, для поддержания необходимой неизменности соотношений физических свойств пространства, кроме собственной энергии самого глобального пространства, в общем случае необходим дополнительный источник энергии, находящийся либо в центре симметрии соответствующего трехмерного гипертора, либо симметрично на его полюсах. Этот дополнительный источник энергии я буду далее называть "Черной дырой Вселенной".
       Кроме того, учитывая аналогию с другими полями, весьма вероятно, что для самого существования глобального пространства Вселенной, как физического поля, необходим источник такого поля, и в качестве такого источника, по-видимому, выступает указанная "Черная дыра Вселенной".
       Поскольку квантовая физика позволяет выдвинуть гипотезу о том, что нелокальные явления и взаимодействия (нелокальная связанность взаимодействовавших частиц (квантовая запутанность), редукция волновой функции, возможно также - туннельный эффект и т.п.) играют важнейшую и недооцененную пока роль в природе любого взаимодействия, то весьма вероятно, что указанная "Черная дыра Вселенной", а точнее количественные значения и соотношения ее физических свойств могут непосредственно и нелокально (мгновенно и не полностью опосредовано через структуру (по крайней мере локальную структуру) пространства) определять некоторые фундаментальные физические свойства материи (отдельные законы физики) или оказывать на них существенное влияние. В первую очередь это касается самого глобального пространства Вселенной, все физические свойства которого (в том числе одинаковые во всем пространстве и неизменные во всем времени), могут в значительной степени определяться не только указанными собственными энергиями, импульсами, моментами импульса самого глобального пространства и прочей возможной его динамикой (течениями, искривлениями, вихрями), вызванной, например, вложенной материей, но и указанными количественными значениями и соотношениями физических свойств "Черной дыры Вселенной".
       Однако для подобной революции и создания соответствующей единой теории поля необходим и новый революционный метод исследования проблемы. Поскольку мы теперь видим, что такая революционная космологическая теория поля тесно связана с указанной главной нерешенной проблемой физики, то именно попытки ее решения на основе самых загадочных и необъяснимых явлений и открытий физики, как раз и могут приблизить нас к созданию этой революционной космологической теории поля.

      
       Часть первая.
       Главная нерешенная проблема физики и нелокальная связанность Вселенной.
      
       При существующих размерах и возрасте Вселенной единственно возможным  объяснением главной проблемы физики с общефилософской точки зрения является вывод о том, что наша Вселенная является нелокально связанным объектом. Это означает, что между всеми и любыми составляющими Вселенной, то есть между всеми и любыми участками ее пространства и между всеми и любыми ее материальными объектами от элементарных частиц и атомов до скоплений и сверхскоплений галактик всегда и постоянно существуют некие специфические взаимодействия, далее называемые нелокальными взаимодействиями, осуществляемые и распространяющиеся в пространстве с бесконечной скоростью. То есть все пространство Вселенной и вся вложенная в это пространство материя всегда нелокально взаимосвязаны и взаимозависимы, как в целом, так и любыми своими частями и составляющими. Именно бесконечность скорости осуществления вышеуказанных нелокальных взаимодействий между всеми и любыми составляющими Вселенной и обеспечивает следующие свойства Вселенной: целостность Вселенной, как единого объекта, означающая взаимосвязанность и взаимозависимость всех ее составляющих; постоянство во времени и одинаковость в пространстве любых физических законов во Вселенной; постоянную самовоспроизводимость Вселенной, включая как все ее пространство и время, так и всю вложенную в это пространство материю, так и все физические законы Вселенной во всем ее пространстве и всем ее времени. Без участия таких нелокальных взаимодействий, распространяющихся в пространстве с бесконечной скоростью, разделенные колоссальными расстояниями отдельные области Вселенной были бы на протяжении колоссального времени настолько независимы и автономны, что не было бы никаких условий и причин существования вышеуказанных свойств Вселенной, включая постоянство во времени и одинаковость в пространстве любых физических законов во Вселенной. Между тем мы видим, например, что всегда и везде в любых квантовых взаимодействиях во Вселенной могут рождаться только элементарные частицы, относящиеся к известным элементарным частицам стандартной модели. Эти указанные нелокальные взаимодействия следует отличать от известных процессов передачи через пространство статистически определенного количества энергии между объектами барионной материи, которые занимают конечное время, и скорость которых ограничена скоростью света в вакууме. В то же время, информацию, по-видимому, возможно передавать между объектами барионной материи, включая черные дыры, через пространство нелокально с бесконечной скоростью. О возможности создания сверхсветового коммуникатора я писал ранее - смотрим серию статей "Сверхсветовой коммуникатор". Нельзя полностью исключить и возможность передачи некоторых недостаточно изученных видов энергии нелокально - с бесконечной скоростью. Так, например, возможно Черная дыра Вселенной может передавать часть или всю свою энергию нелокально - с бесконечной скоростью - во все точки пространства Вселенной, обеспечивая расширение этого пространства. Но, все же, несоизмеримо более вероятно, что любые формы энергии в статистически определенных количествах могут передаваться через пространство со скоростями не превышающими скорости света в вакууме. На это, прежде всего, указывают факты, говорящие о том, что радиус риманова пространства Вселенной растет со скоростью равной скорости света в вакууме; подробнее я это обосную это положение в последующих частях настоящей статьи. В то же время, взаимодействие объектов Вселенной в виде нелокального, осуществляемого с бесконечной скоростью, преобразования одних видов энергии в другие совместно с нелокальной передачей информации является более предпочтительным механизмом  осуществления нелокальной связанности этих объектов. Впрочем, на данной стадии осмысления данной гипотезы конкретный механизм осуществления нелокальной связанности объектов Вселенной не важен. В философском и методологическом плане для нас важно понимание того факта, что локальность и нелокальность есть неразделимые диалектические противоположности не существующие друг без друга (о диалектике локального и нелокального я еще упомяну в части третьей настоящей статьи), и безусловно теснейшим образом связанные в законах физики, большинство из которых мы еще не постигли. В непосредственном практическом плане для нас пока достаточно тех знаний, которые уже дает нам квантовая физика, об этом немного ниже. Изложенную в этой главе гипотезу (о том, что Вселенная является таким нелокально связанным объектом, обладающим такими специфическими взаимодействиями, распространяющимися в пространстве с бесконечной скоростью, и о соответствующих перечисленных свойствах Вселенной) я называю "Принципом нелокальной связанности Вселенной", или для краткости "нелокальной связанностью Вселенной".
        Реальное подтверждение этой гипотезы  ("Принципа нелокальной связанности Вселенной") нам дает квантовая физика. Из нее для нас наиболее важны два научно установленных физических закона, подтверждающие наличие таких нелокальных взаимодействий, протекающих и распространяющихся в пространстве с бесконечной скоростью. Первым является закон редукции (происходящей с бесконечной скоростью) волновой функции, а вторым - закон нелокальной связанности взаимодействовавших квантовых частиц. Эти подтверждения дают нам основания считать, что именно квантовые свойства Вселенной, обеспечивающие наличие указанных нелокальных взаимодействий, и, в первую очередь, квантовые  свойства самих пространства и времени Вселенной обеспечивают нелокальную связанность Вселенной.
       Таким образом, "Принцип нелокальной связанности Вселенной" также дает основание считать, что Вселенная в целом и, в том числе, пространство и время Вселенной являются сугубо квантовыми объектами, что не лишает нас возможности во многих аспектах и в некоторых приближениях рассматривать их как классические объекты и применять к ним с достаточной степенью осторожности законы и принципы классической физики.

      
       Часть вторая.
       Главная нерешенная проблема физики и гипотеза квантовой стабильности.
      
       На основе принципа нелокальной связанности Вселенной, и с учетом того, что Вселенная является сугубо квантовым объектом, естественно предположить, что одинаковость в пространстве и неизменность во времени всех физических законов и универсальных физических констант, в том числе неизменность и одинаковость набора элементарных частиц, объясняется тем, что пространство Вселенной вместе со всей вложенной в это пространство материей является единым квантовым объектом. Это означает, что вся вложенная в пространство Вселенной материя описывается, как  решение, а само пространство Вселенной во времени также, как и любая отдельная элементарная частица стандартной модели (кварки, лептоны и калибровочные бозоны) описывается не просто как решение, а еще и как соответствующая собственная функция одного и того же глобального квантового уравнения или глобальной системы квантовых уравнений (в общем случае уравнение всегда сводимо к системе уравнений) для соответствующих начальных условий.
        При поверхностном прочтении такую гипотезу могут назвать секретом Полишинеля, де "конечно же наверное вся Вселенная может быть описана невероятно чудовищно сложным квантовым уравнением, которое невозможно составить". Но речь в основном не об этом. Я полагаю, что существует довольно простое квантовое уравнение (система уравнений), решение которого для пространства Вселенной в целом достаточно достоверно описывает общую динамику пространства Вселенной, и которое является одной из собственных функций этого уравнения. При этом другими собственными функциями этого довольно простого квантового уравнения являются, как это ни странно, поля (волновые функции) свободных (а иногда возможно и связанных) элементарных частиц стандартной модели, причем локализация этих полей в пространстве и времени Вселенной без учета прочей материи описывается сравнительно небольшим (вероятно от четырех до десяти) набором параметров.
       Наличие этих собственных функций и решений одного и того же глобального квантового уравнения, в силу существования известных нелокальных квантовых взаимодействий (указанные: закон редукции (происходящей с бесконечной скоростью) волновой функции; закон нелокальной связанности взаимодействовавших квантовых частиц), а также в силу существования еще не известных нелокальных квантовых взаимодействий, означает указанную мгновенную, то есть происходящую с бесконечной скоростью, взаимосвязанность и взаимозависимость вообще любых объектов и частей Вселенной. Такие взаимосвязанность и взаимозависимость обеспечивают указанные свойства Вселенной: целостность и воспроизводимость Вселенной; одинаковость в пространстве всех физических законов, в том числе всех универсальных физических констант и набора элементарных частиц. А достаточная стабильность указанных начальных условий, проявляющихся в виде самовоспроизводящейся во времени глобальной геометрии пространства, обеспечивает неизменность во времени всех физических законов, в том числе всех универсальных физических констант и набора элементарных частиц. Данное объяснение неизменности во времени и одинаковости в пространстве законов физики я далее для краткости буду называть "Гипотеза глобальной квантовой самовоспроизводимости и стабильности Вселенной" или еще короче "Гипотеза квантовой стабильности".


       Часть третья.
       Нелокальная связанность Вселенной, гипотеза квантовой стабильности и диалектика Гегеля.

       Хотя указанный квантовый подход и "Гипотеза квантовой стабильности" означает, что каждая элементарная частица, как и каждый материальный объект Вселенной, описываются с помощью неких глобальных "единого глобального гамильтониана Вселенной" и "единого глобального вектора состояния" (или "глобальной матрицы плотности") Вселенной, это не исключает для нас возможности ограничивать задачу небольшим существенным участком пространства и времени Вселенной, и, правильно формулируя начальные и граничные условия для этого участка, получать для такого участка правильные решения с помощью известных ранее законов квантовой физики. Таким образом, воспроизводимость локальной геометрии пространства, локально сохраняющего все геометрические соотношения и свойства нелокально самовоспроизводимой глобальной геометрии всего пространства Вселенной, позволяет с достаточной степенью точности и предсказательности правильно решать соответствующие квантовые задачи для локально ограниченной области пространства и времени и вложенной в них материи. Но сама эта локальная возможность существует именно вследствие указанной нелокальной самовоспроизводимости глобальной геометрии всего пространства Вселенной вместе со всей вложенной в это пространство материей.
       В вышеприведенном рассуждении мы видим присутствие всех философских диалектических Гегелевских законов взаимодействия и развития противоположных сущностей, коими в указанном аспекте являются локальность и нелокальность. Кроме того, квантовый подход исключает любую механистическую детерминированность, и уж тем более фатализм. Я считаю, что он исключат даже многомировую интерпретацию, представляющую из себя крайне надуманную фантазию. Как раз именно квантовый подход и обеспечивает Гегелевское диалектическое единство таких противоположных сущностей, как закономерность и случайность. К сожалению со смертью натурфилософии и с переходом в естествознании к жестким принципам практической и опытной верификации из естествознания были практически волюнтаристски вытравлены все достижения и принципы материалистической и диалектической философии, забывая о том что эти достижения прошли такой длинный путь практической и опытной верификации, перед которым меркнет путь даже самого естествознания. Под лозунгами рационализма, позитивизма и борьбы с философией в естествознании, которые сами являются философией, причем философией самого низкопробного демагогического и политиканского пошиба, из естествознания были предательски вытравлены сильнейшие механизмы познания и глобального анализа явлений природы.


       Часть четвертая.
       Гипотеза квантовой стабильности и принципы выбора геометрии пространства-времени в первом приближении.

             Для проверки "Гипотезы квантовой стабильности" в первом приближении необходимо выбрать максимально реалистичную (максимально соответствующую реально наблюдаемой физической картине Вселенной) модель геометрии глобального пространства Вселенной. Кроме того, необходимо правильно составить для этой выбранной геометрии квантовое уравнение (уравнение Шредингера) для вектора состояния пространства, найти для этого уравнения собственные функции и собственные числа, соответствующие данной выбранной модели геометрии пространства и реально существующим элементарным частицам.
       Решение этой задачи невозможно без выяснения и определения геометрии глобального пространства-времени Вселенной. В общефизическом и общефилософском смысле именно единство в пространстве и неизменность во времени законов эволюции пространства Вселенной и обеспечивает вкупе с "Принципом нелокальной связанности Вселенной" неизменность всех физических законов во времени. Для того, чтобы выяснить указанную геометрию, не привязывая себя к крайне упрощенной фридмановской модели, которая не учитывает изначальную глобальную анизотропию и изначальную глобальную неоднородность Вселенной, нам необходимо уйти от постулируемого общей теорией относительности невероятно усложняющего геометрическую картину Вселенной пространственно-временного многообразия и равноправия всех инерциальных систем отсчета. В настоящее время в космологии базовой общепринятой моделью геометрии Вселенной является так называемая "плоская" (евклидова, то есть не криволинейная) модель Лямбда-CDM космологической теории, на самом деле являющейся замысловатой компиляцией теорий темной энергии (лямбда) и темной материи (CDM), и изначально опирающейся на постулируемую общей теорией относительности евклидовую (плоскую) геометрию базового, то есть лишенного материи, пространства. В этом смысле Лямбда-CDM космологическая теория является своеобразной тавтологической подгонкой под собственный базовый постулат об отсутствии крупномасштабной кривизны базового пространства. Под этот постулат и подгоняются величины и процентные соотношения темной энергии, темной материи и барионной материи; сюда же втискивается и сравнительно малая неоднородность и анизотропия реликтового излучения. В то же время этой теорией полностью игнорируются последние данные о наличии у Вселенной собственного момента импульса, подтвержденные, по крайней мере, на масштабах сверхскопления Девы и ближайших сверхскоплений галактик. Рассуждения же и некоторые расчеты, говорящие о сравнительно малой неоднородности и анизотропии реликтового излучения являются схоластическими, поскольку не проверялись аналогичным образом для криволинейных моделей пространства, в том числе для геометрий пространства в виде трехмерной гиперсферы или трехмерного гипертора. В то же время, немногочисленные работы по проверке соответствия угловых корреляционных функций температурных флуктуаций реликтового излучения (космического микроволнового фона), рассчитанных для моделей трехмерных гиперсферического и гипертороидального пространства, дают значительно большее совпадение с реальным реликтовым излучением, чем соответствующие функции, рассчитанные для модели евклидова (плоского) пространства, но соответствующие работы по большей части игнорируются сторонниками Лямбда-CDM космологической теории. Доказательность здесь уступила консенсусу. Между тем, серьезнейшие проблемы физики еще никогда удавалось решить методом некого мажоритарного голосования. Поэтому отказ от такой евклидовой (плоской) модели и от постулируемого общей теорией относительности невероятно усложняющего геометрическую картину Вселенной пространственно-временного многообразия и равноправия всех инерциальных систем отсчета необходим нам, чтобы понять каким образом изменяется и развивается неевклидовая (криволинейная) геометрия (топология) глобального пространства в неком глобальном времени общем для всех точек геометрии этого глобального пространства, а потому выделяющем глобальное пространство в качестве абсолютной выделенной системы отсчета. При этом для каждой отдельной собственной (покоящейся) точки геометрии этого глобального пространства оказывается возможным ввести свою абсолютную локальную и уже евклидовую инерциальную систему отсчета, покоящуюся относительно данной точки, время в которой течет также, как и глобальное время. Для любого движущегося (относительно глобального пространства) наблюдателя его собственное время определяется через глобальное время и его скорость относительно глобального пространства. Таким образом локальное (предельно малое) приращение времени для движущегося (относительно глобального пространства) наблюдателя, находящегося в данный момент времени в некоторой собственной (покоящейся) точке глобального пространства, определяется через соответствующее приращение времени в указанной абсолютной евклидовой локальной системе отсчета в этой точке, которое равно приращению глобального времени (в силу локально одинакового течения времени), точно так же как и в специальной теории относительности, поскольку четырехмерная метрика глобального пространства-времени  является для непрерывного пространства-времени локально приводимой к метрике Минковского.


       Часть пятая.
       Главная нерешенная проблема физики и соотношения масштаба.

       Для решения указанной проблемы важным также является вопрос о том, может ли некое глобальное материальное физическое тело (например глобальная черная или белая дыра Вселенной), существующее в глобальном пространстве-времени Вселенной, а конкретнее некие соотношения масштаба, понимаемые, как соотношения его физических свойств определять и обеспечивать наблюдаемые характеристики этого пространства-времени и, с учетом нелокальной связанности Вселенной, упомянутую неизменность и одинаковость всех физических законов природы во всем пространстве-времени Вселенной за счет того, что все или многие свойства пространства-времени и все или многие физические законы природы определяются физическими характеристиками этого глобального материального физического тела.
       В связи с предыдущим вопросом важен также и вопрос о том, могут ли некие соотношения масштаба глобального пространства-времени, а именно сами геометрические соотношения и пропорции глобального пространства-времени, в том числе соотношения и пропорции его динамических свойств (движений, вращений, колебаний), влиять или даже определять все остальные свойства пространства-времени и все физические законы природы или хотя бы значительную их часть.
       В свете вышесказанного ответ на эти вопросы уже интуитивно ясен. Такие соотношения масштаба не только могут, но и должны определять все остальные свойства пространства-времени и все физические законы природы, поскольку определять их больше не чему. Именно поэтому и евклидова (плоская) геометрия и любая чисто гиперсферическая геометрия не подходят на роль глобальной геометрии пространства и пространства-времени, поскольку изначально лишены подобных соотношений масштаба.


       Часть шестая.
       Теория глобального времени, как фундамент для выбора глобальной геометрии пространства-времени Вселенной.

       Предлагаемая для решения указанной проблемы концепция глобального пространства-времени Вселенной опирается на концепцию пространства и концепцию "глобального времени", разработанную и изложенную выдающимся российским ученым Дмитрием Евгеньевичем Бурланковым в его работах «Динамика пространства» (2005г.) и «Теория глобального времени», изданных в России Нижегородским государственным университетом им. Н.И. Лобачевского. Данные работы Д.Е. Бурланкова являются обобщением и развитием «Общей теории относительности» А. Эйнштейна и Д. Гилберта, которая вытекает из «Теории глобального времени», как частный случай - при равенстве нулю суммы собственной плотности энергии пространства и прочей вложенной в пространство энергии.
       В указанных и других своих работах, посвященных динамике пространства, Д.Е. Бурланков вводит и обосновывает понятие "глобального времени", как времени единого (одинакового) для всех точек динамически меняющегося трехмерного пространства, уравнения для метрики которого в "глобальном времени" вытекают, как аналогично и у Д. Гилберта (в отличие от Бурланкова, Гилберт выводит свои уравнения не для метрики трехмерного пространства, а для метрики четырехмерного пространства-времени Минковского, что порождает некоторую тавтологичность и ограниченность общей теории относительности), из применения вариационного принципа наименьшего действия для лагранжиана, представляющего собой разность собственных кинетической и потенциальной энергии пространства, выражаемых через метрику пространства, с поправкой на действие прочей материи. Однако, для обеспечения полноты и "решаемости" полученной системы из девяти нелинейных уравнений второго порядка в частных производных для метрики пространства-времени, и Д.Гилберту и А. Эйнштейну пришлось искусственно вводить дополнительное - десятое уравнение связи, накладывающее ограничение на плотность энергии, а именно - сумма собственной плотности энергии пространства и плотности энергии вложенной материи должна быть равна нулю, чего вовсе не следовало ни из каких экспериментальных данных, и что опровергается новейшими наблюдениями. Но Д.Е. Бурланкову, за счет введения единого "глобального времени" для метрики трехмерного пространства, удалось сформулировать и решить вариационную задачу в "глобальном времени", и получить для трехмерной метрики пространства полную и решаемую систему из шести динамических нелинейных уравнений второго порядка в частных производных и трех линейных по скорости уравнений связи для поля скоростей, то есть без введения каких-либо надуманных дополнительных уравнений связи и ограничений на суммарную плотность энергии, в том числе без ее искусственного обнуления.
       При этом, Д.Е. Бурланков не только находит и во много раз расширяет круг и классы возможных решений уравнений для метрики пространства, благодаря чему объясняет необъясненные до него явления, но и существенно упрощает вид решений, уже полученных в рамках Общей теории относительности, за счет введения единого "глобального времени" и ухода от невероятно усложняющего картину пространственно-временного четырехмерного многообразия.
       "Глобальное время" используется Д.Е. Бурланковым как для решения задач для пространства любой отдельной свободно падающей локальной микро-лаборатории - лаборатории с однородным в бесконечно-малом пределе пространством, так и для получения отдельных классов решений макроскопических задач с определенным классом граничных (начальных) условий и источников энергии.
       Д.Е. Бурланков называет собственную энергию пространства гравитационной, вводит для описываемого им пространства "абсолютную инерциальную систему", в которой точки пространства своих координат не меняют (используемую в "динамической геометрии"), и математически доказывает, что постулируемое им первоначально для всего пространства бесконечно малой микро-лаборатории единое "глобальное время" является единым и одинаково текущим для любых и всех вместе свободно падающих в гравитационном поле "глобального пространства" локальных микро-лабораторий. Он находит решения для вращения отдельных областей пространства и для вращения всего Мира (Вселенной), а также решения для вихрей пространства в масштабах галактик и их скоплений, которые, как он объясняет, вполне могут претендовать на роль темной материи. Он вводит понятия "глобальное время Мира" и "глобальное пространство Мира", в классическом и квантовом виде формулирует и решает космологические задачи для динамики пространства Мира (Вселенной) для фридмановской модели пространства (трехмерной сферы переменного радиуса). При этом ему удается уйти от проблемы критической плотности материи в космологии и обойти необходимость введения темной энергии. Согласно его решениям Мир (Вселенная) может быть открытым или закрытым независимо от плотности находящейся в нем материи.


       Часть седьмая.
       Основания выбора геометрии трехмерного гипертора в качестве глобальной геометрии пространства-времени Вселенной.
      
       Однако, для объяснения ряда наблюдаемых во Вселенной явлений, в которых проявляется ее глобальная анизотропия и глобальная неоднородность, Фридмановская модель Вселенной в виде трехмерной гиперсферы переменного радиуса (3-сферы), на которую, при решении глобальной космологической задачи, опирается и Бурланков, на мой взгляд, является чрезмерно упрощенной. Полагаю, что гораздо более полную теорию, объясняющую наблюдаемые явления, мы получаем при использовании модели пространства Вселенной в виде трехмерного гипертора, у которого радиус третьей образующей окружности много больше как радиуса второй образующей окружности, так и радиуса третьей образующей окружности  (R1<<R3 и R2<<R3); такой трехмерный гипертор далее я буду называть квази-гиперсферическим трехмерным гипертором. Такой квази-гиперсферический трехмерный гипертор может быть недеформированным (или мало-деформированным), а значит самопересекающимся и имеющим четыре, а в вырожденном случае R1=0 (радиус первой образующей окружности равен нулю) две вложенных друг в друга трехмерных поверхности близких к трехмерным гиперсферам (за исключением областей близких к полюсам (x3=R3 и x4=R3)). Такой трехмерный гипертор может быть не самопересекающимся, но сферически деформированным, само-соприкасающимся (закрытым в точку в его центре симметрии или в окружность, или в двумерную сферическую или двумерную тороидальную поверхность). Возможны и иные смешанные геометрии в виде самопересекающегося, но значительно сферически деформированного трехмерного гипертора со значительной сферической деформацией отдельных областей самопересечения (например областей близких к трехмерным гиперсферам). Такой гипертор является трехмерной поверхностью в четырехмерном евклидовом пространстве его построения, то есть он является трехмерной поверхностью соответствующего четырехмерного гиперполнотория. Необходимость его сферической деформации я поясню немного ниже (в части восьмой настоящей статьи).
       А теперь подробнее обоснуем необходимость выбора геометрии трехмерного гипертора в качестве модели геометрии глобального пространства. Дело заключается в следующих отличиях геометрии трехмерного гипертора как от геометрии Фридмановской трехмерной гиперсферы, так и от геометрии евклидового (плоского) пространства:
       Во-первых, в геометрию трехмерного гипертора уже изначально заложены глобальная анизотропия и глобальная неоднородность, которые свойственны нашей Вселенной, и доказательства существования которых я также приведу немного ниже (в части девятой настоящей статьи).
       Во-вторых, центр симметрии закрытого в точку (само-соприкасающегося в его центре симметрии) трехмерного гипертора принадлежит его собственной трехмерной поверхности (находится в области его собственного трехмерного пространства) в отличие от трехмерной гиперсферы, поэтому такой центр симметрии, содержащий, например, глобальный сверхмассивный энергетический объект (Черную дыру Вселенной), может определять (вкупе с самим остальным пространством Вселенной) важнейшие физические законы и универсальные физические константы для всей Вселенной и быть реальным источником темной энергии и темной материи для трехмерного пространства Вселенной. В более общем случае такой трехмерный гипертор может быть самопересекающимся  в области его центра симметрии, но область пересечения должна быть достаточно малой, чтобы она полностью охватывалась этим глобальным сверхмассивным энергетическим объектом (Черной дырой Вселенной), а сферическая деформация могла бы проявлять себя в достаточной степени. В случае В рамках же гипер-сферического пространства (пространства в виде трехмерной гиперсферы) нам не удастся поместить глобальный гравитирующий объект (Черную дыру Вселенной) в геометрический центр этого гипер-сферического пространства и, в то же время, остаться на поверхности соответствующего четырехмерного гипер-шара, которая и будет при этом являться наблюдаемым гипер-сферическим трехмерным пространством. То есть такой глобальный объект неизбежно при этом оказывается вне наблюдаемого трехмерного пространства.
       Даже в случае глобального пространства в виде квази-гиперсферического (R1<<R3 и R2<<R3) самопересекающегося недеформированного (или мало-деформированного) трехмерного гипертора, указанная Черная дыра Вселенной может быть расположена симметрично (в виде двух или четырех объектов) на полюсах (x3=R3 и x4=R3) такого трехмерного гипертора, что невозможно в случае трехмерной гиперсферы, поскольку у нее нет геометрических полюсов.
       В-третьих, как гипер-сферическая геометрия пространства, так и евклидова (плоская) геометрия не предполагают наличия каких бы то ни было геометрических соотношений масштаба, поскольку единственной геометрической характеристикой гиперсферы является ее радиус соответствующей гиперсферы, который не с чем соизмерять и сравнивать. Для евклидова пространства дело обстоит еще хуже. Евклидова геометрия вообще не предполагает наличия каких-либо собственных радиусов пространства. В то же время применительно к теории Большого взрыва, у барионной материи и излучения должны существовать единственная граница и единственный радиус в безграничном евклидовом пространстве, определяемые временем существования Вселенной после Большого взрыва. Таким за пределами такого радиуса постулируется существование пространства в форме отсутствия какой бы то ни было материи, что уже само по себе является неразрешимым парадоксом. Очевидно, что никаких геометрических соотношений масштаба для такой евклидовой геометрии также не существует. Но именно соотношения масштаба и должны определять все основные физические законы пространства и законы развития геометрии пространства во времени. В то же время гипер-тороидальная геометрия имеет большое множество различных соотношений масштаба, к которым относятся различные соотношения следующих геометрических и соответствующих физических величин: радиусов трех образующих окружностей  трехмерного гипертора; скоростей и ускорений изменения этих радиусов; степени сферической и (или) иной деформации трехмерного гипертора, скоростей и ускорений изменения этих степеней; скоростей вращений, скоростей и амплитуд вращательных колебаний его пространства вдоль его трех  образующих окружностей; степенные функции указанных величини, и т.д. Само наличие указанных динамических движений, по-видимому, и обеспечивает существование практически всех физических величин, таких как: масса, импульс, момент импульса, энергия, заряд, гравитационные, электрические, слабые и сильные взаимодействия, и т.д. Кроме того, если рассматривать традиционную теорию "Большого взрыва" в рамках однородного и изотропного (кроме направления времени) "плоского" (не криволинейного) глобального базового пространства-времени или же в рамках гипер-сферического глобального пространства, которое также является однородным и изотропным (кроме направления времени), то у точечного изначального источника энергии Вселенной нет никаких математических оснований к саморазвитию вследствие отсутствия соотношений масштаба в однородном и изотропном (кроме направления времени) пространстве-времени. Для такого точечного источника энергии трехмерное однородное и изотропное пространство, в том числе гипер-сферическое пространство, неотличимы от одномерного пространства, и даже единственно возможное в таких условиях соотношение масштаба R=T*C (где T - глобальное время, а C - скорость света в вакууме) оказывается лишенным смысла, вследствие отсутствия масштабированной линейки для измерений пространства и времени и соответствующих величин для сравнения и сопоставления, в том числе для сопоставления масштабов. Именно поэтому я полагаю, что Большой взрыв и последующее появление и саморазвитие неоднородной и анизотропной Вселенной невозможны в однородном и изотропном (кроме направления времени) пространстве-времени.


       Часть восьмая.
       Необходимость квази-гиперсферичности (R1<<R3 и R2<<R3) либо сферической деформации трехмерного гипертора, используемого в качестве модели глобальной геометрии пространства-времени Вселенной.

       Сразу же необходимо пояснить, что сферическая деформация нашего трехмерного гипертора (пространства Вселенной) необходима нам для соответствия предлагаемой модели ряду фактов в наблюдаемой картине Вселенной. А именно:
       Во-первых, на крупных масштабах соответствующих примерно десяткам сверхскоплений галактик, пространство Вселенной наблюдается, как достаточно однородная структура, за малым количеством наблюдаемых исключений, проявляющих себя, как указание на наличие во Вселенной одной или нескольких выделенных осей (подробнее об этом немного ниже).
       Во-вторых, самые удаленные из наблюдаемых галактик, находятся от нас примерно на одинаковом расстоянии, равном в световых годах условному возрасту Вселенной, и удаляются от нас примерно с одной и той же скоростью близкой к скорости света в вакууме. Действительно, согласно современным представлениям наиболее удаленный от нас наблюдаемый объект во Вселенной - галактика GN-z11 - расположен на расстоянии от нас около 13,4 миллиардов световых лет. Почти на таком же расстоянии расположены от нас и другие максимально удаленные от нас объекты по всем направлениям в пространстве. Возраст Вселенной оценивается астрофизиками в величину примерно 13,8 миллиардов лет. Следовательно, средняя скорость удаления от нас этого объекта и других максимально удаленных объектов по другим направлениям в пространстве близка к скорости света. С высочайшей степенью вероятности, мы не проживаем случайно именно в то время, когда средняя скорость удаления от нас этих максимально удаленных объектов по всем направлениям в пространстве почти совпала со скоростью света. Следовательно, наиболее вероятно, что скорость удаления от нас этих максимально удаленных объектов по всем направлениям в пространстве всегда была близка к скорости света.
       В-третьих, априори Земля не является центром Вселенной, следовательно, для любой точки (объекта) во Вселенной выполняется то же правило, что и для Земли, а именно: наиболее удаленные от любого объекта по всем направлениям другие видимые объекты во Вселенной находятся от него на расстоянии немного меньше, чем 13,8 миллиардов световых лет и удаляются от него со скоростью немного меньшей скорости света.
       В-четвертых, за все время наблюдений ни одна из наблюдаемых далеких галактик не скрылась из вида, и, по-видимому, в поле возможной видимости не появляется новых галактик, что указывает на высокую степень постоянства скорости их удаления.
       В-пятых, как известно существует "расстояние до поверхности последнего рассеяния". Это расстояние от Земли, до поверхности, за которой вся (в основном) первоначальная (образованная сразу после Большого взрыва) полностью ионизированная водородно-гелиевая плазма рекомбинировала с образованием нейтральных атомов и стала прозрачной для микроволнового излучения, образованного в результате рекомбинации атомов водорода (захвата протоном электрона на атомную орбиту). Так вот это расстояние, согласно последним данным наблюдений за указанным микроволновым излучением, называемым также "реликтовым излучением", либо "космическим микроволновым фоном", равно 3,1486 Хаббловских длин. Читателя с "незамыленным" взглядом сразу же должна насторожить "подозрительная" близость только что указанного числа 3,1486 к числу пи равному 3,1415... . А Хаббловская длина, как известно, равна расстоянию, которое свет в вакууме проходит за время возраста Вселенной равного 13,8 миллиардов световых лет. Как известно, "расстояние до поверхности последнего рассеяния" (от Земли) немного меньше "расстояния до горизонта частиц". "Расстояние до горизонта частиц" определяется в световых годах, как время за которое свет пройдет от Земли до максимально удаленных объектов во Вселенной при условии, что Вселенная при этом не будет расширяться. (Методы расчета этого расстояния вызывают у меня большие сомнения, но, тем не менее, я воспользуюсь известным общепризнанным мнением, что "расстояние до горизонта частиц" может быть равно "горизонту частиц", то есть расстоянию в реальном трехмерном пространстве Вселенной между максимально удаленными возможными объектами во Вселенной.) При этом следует различать понятия "горизонт частиц" и "расстояние до горизонта частиц" (расстояние от Земли), которое иногда путают даже серьезные астрономы. Если полагать, что глобальное пространство Вселенной евклидово ("плоское"), то "расстояние до горизонта частиц" (расстояние от Земли) определяется расстоянием от Земли до центра шара, являющегося нашей Вселенной. Если полагать, что Земля находится в центре этого шара, то "расстояние до горизонта частиц" в два раза меньше "горизонта частиц"; а если полагать, что Земля находится на краю этого шара, то есть максимально удалена от его центра, то "расстояние до горизонта частиц" равно "горизонту частиц". Поскольку "расстояние до горизонта частиц" немного больше "расстояния до поверхности последнего рассеяния", то получается, что если Земля находится на краю вышеуказанного шара, являющегося нашей Вселенной", то "горизонт частиц" равен "расстоянию до горизонта частиц", и расстояние в реальном трехмерном пространстве Вселенной между максимально удаленными возможными объектами во Вселенной, равное диаметру вышеуказанного трехмерного шара, примерно равно 3,1486 Хаббловских длин (Хаббловская длина в световых годах - возраст Вселенной). (В световых годах это расстояние равно 3,1486 умножить на 13,8 миллиардов сетовых лет, то есть равно 43,45 миллиардов световых лет.) То есть, при предположения (условии), что пространство Вселенной евклидово ("плоское") и, что Земля находится на краю вышеуказанного шара, то получается, что диаметр вышеуказанного трехмерного шара, являющегося нашей Вселенной,  в световых годах в 3,1486 раз больше возраста Вселенной. В этом случае радиус Вселенной в световых годах в 1,5743 раз больше возраста Вселенной, что невозможно без вывода о том, что радиус Вселенной когда-то рос, со скоростью, превышающей скорость света в вакууме. Если же предположить, как считают некоторые авторы, что Земля и в такой "плоской" геометрии является не краем, а центром Вселенной, и что "горизонт частиц" в два раза дальше "расстояния (от Земли) до горизонта частиц", то ситуация для "плоской" (евклидовой) геометрии еще хуже, поскольку в этом случае мы должны считать, что "горизонт частиц" в два раза больше "расстояния до горизонта частиц", а радиус Вселенной в световых годах в 3,1486 раз больше возраста Вселенной. Указанные противоречия и натяжки сразу же автоматически снимаются в предположении, что геометрия глобального пространства Вселенной является гиперсферической либо квази-гиперсферической, например, является геометрией квази-гиперсферического (R1<<R3 и R2<<R3), либо сферически деформированного трехмерного гипертора. Для такой геометрии "горизонт частиц" автоматически совпадает с "расстоянием до горизонта частиц" и равен диаметру указанной трехмерной гиперсферы или квази-гиперсферы, то есть "горизонт частиц" попросту числу пи (3,1415...) умноженному на радиус соответствующей трехмерной гиперсферы или соответствующей квази-гиперсферической трехмерной поверхности. Дело здесь в том, что любая точка на трехмерной поверхности гиперсферы, как и любая точка на поверхности обычной двумерной сферы не является ни ее центром, ни ее краем. В то же время, поскольку "расстояние до горизонта частиц" немного больше "расстояния до поверхности последнего рассеяния", то получается, что диаметр указанной трехмерной гиперсферы или квази-гиперсферы, равный "горизонту частиц", равен в сетовых годах Хаббловской длине (возрасту Вселенной) умноженной на 3,1486. Это означает, что радиус указанной трехмерной гиперсферы или квази-гиперсферы, являющейся пространством нашей Вселенной, примерно равен Хаббловской длине, а точнее равен Хаббловской длине, умноженной на 1,00226, то есть на отношение близкой к числу пи указанной величины равной 3,1486 к самому числу пи (3,1415...). Поскольку методы определения указанной величины 3,1486 не дают надежды на ее достоверное определения с точностью до третьего знака после запятой, то мы можем с полным основанием и с хорошей точностью считать, что если пространство нашей Вселенной является трехмерной гиперсферой или кваз-гиперсферой, то радиус этой гиперсферы или кваз-гиперсферы равен Хаббловской длине, то есть в световых годах равен возрасту Вселенной. В такой геометрии Вселенной "горизонт частиц" равен половине длины окружности с радиусом раным Хаббловской длине (возрасту Вселенной).
       Таким образом, вышеуказанный экспериментально  обнаруженный факт, что расстояние до поверхности последнего рассеяния равно 3,1486 (почти пи) Хаббловских длин, получает естественное "геометрическое" объяснение. Кроме того, такая геометрия означает, что радиус соответствующей трехмерной гиперсферы или соответствующей квази-гиперсферической трехмерной поверхности, являющейся пространством нашей Вселенной, совпадает с Хаббловской длиной, а также что этот радиус все время существования Вселенной рос со средней скоростью равной скорости света в вакууме. Поскольку у нас нет оснований полагать, что мы случайно проживаем именно в тот момент времени, когда средняя скорость роста этого радиуса совпала со скоростью света в вакууме, то это практически со сто процентной вероятностью означает, что указанный радиус всегда рос со скоростью равной скорости света в вакууме. Таким образом, мы приходим к первому соотношению масштаба: радиус соответствующей трехмерной гиперсферы или соответствующей квази-гиперсферической трехмерной поверхности, являющейся пространством нашей Вселенной, совпадает с Хаббловской длиной, и растет практически равномерно во времени со скоростью равной скорости света в вакууме, которая является практически постоянной за все время существования Вселенной.

       Уже первые четыре вышеперечисленных факта (перечисленные после слов: во-первых; во-вторых; в-третьих; в-четвертых) практически невозможно объяснить никакой иной геометрией глобального пространства Вселенной, кроме его геометрии  именно в виде трехмерной гиперсферы, либо геометрией близкой к ней, включая геометрию недеформированного (либо мало-деформированного) трехмерного гипертора, у которого радиус третьей образующей окружности много больше как радиуса второй образующей окружности, так и радиуса третьей образующей окружности. Также геометрией близкой к геометрии трехмерной гиперсферы является геометрия сферически деформированного трехмерного гипертора, у которого радиус третьей образующей окружности много больше как радиуса второй образующей окружности, так и радиуса третьей образующей окружности. При этом радиус такой трехмерной гиперсферы (глобального пространства Вселенной), в том числе трехмерной гиперсферы, которой мы аппроксимируем в соответствующей глобальной части наш трехмерный гипертор, должен расти со временем согласно формуле R=T*C, где T - глобальное время Вселенной, а C - скорость света в вакууме, R -радиус нашей трехмерной гиперсферы (глобального пространства Вселенной).
       Простейшее геометрическое построение подтверждает этот вывод. При такой геометрии в электромагнитных волнах (фотонах) мы можем наблюдать только одно полушарие, (а точнее гипер-сферический угол равный 2 радиана, то есть примерно 120 градусов, что меньше полушария с углом равным 180 градусов), трехмерной поверхности такого сферически деформированного объемного четырехмерного гиперполнотория. При этом мы, находясь в геометрическом центре такого полушария, всегда будем наблюдать, что одни и те же максимально удаленные видимые нами галактики и звезды будут всегда удаляться от нас со скоростями почти равными скорости света и не будут исчезать из вида, но при этом на горизонте Вселенной не будут появляться новые галактики и звезды, которых ранее было невозможно увидеть, что собственно пока и наблюдается.

       Все другие виды геометрии глобального пространства я полагаю невозможными, поскольку для соответствия указанным фактам они требуют слишком большого количества искусственных допущений. Например, "плоская" (евклидова, то есть не криволинейная) модель Лямбда-CDM космологической теории, уже потребовала предположения о довольно сложной, а потому крайне маловероятной динамике расширения Вселенной, а именно о первоначальной космической инфляции глобального пространства (расширение всего пространства со скоростями превышающими скорость света в вакууме), а также о смене замедленного расширения на ускоренное расширение. Полагаю, что недостаточность наблюдаемого красного смещения для объяснения малой светимости соответствующих стандартных свечей имеет куда более прозаическое объяснение, чем увеличение плотности неизвестно откуда берущейся темной энергии. Например, в ранней Вселенной химический состав ядра стандартной свечи мог существенно отличаться от его состава в зрелой и поздней Вселенной, что и приводило к более раннему взрыву, то есть к отклонению от современного стандарта. Не исключено, что и существенно большая кривизна глобального пространства в ранней Вселенной так же могла приводить к более раннему взрыву, то есть к отклонению стандартной свечи от современного стандарта.
 
      Сразу же оговорюсь, что, для модели сферически деформированного трехмерного гипертора, на начальной стадии расширения Вселенной (или на начальной стадии очередного цикла ее развития), сферическая деформация мною не постулируется, но я полагаю, что она возникает, как необходимый этап развития глобального пространства Вселенной.
       Однако, именно наблюдаемые исключения из этих фактов, а также иные факты, указывающие на наличие глобальной анизотропии и глобальной неоднородности Вселенной и самого глобального пространства Вселенной (подробнее об этом немного ниже), побуждают нас использовать несколько более сложную, но гораздо лучше объясняющие наблюдаемую картину Вселенной, геометрию глобального пространства Вселенной в виде в виде закрытого (само-соприкасающегося или самопересекающегося в области близкой к его центру симметрии) сферически деформированного трехмерного гипертора.
       Далее я обосную, что необходимым условием указанной сферической деформации нашего трехмерного гипертора являются условия: R1<<R3 и R2<<R3, где R1, R2 и R3 соответственно радиусы первой, второй и третьей образующей окружности (соответствующие образующие радиусы) нашего трехмерного гипертора. Знак << здесь и далее означает много меньше. При этом радиус третьей образующей окружности (третий образующий радиус) R3 нашего трехмерного гипертора по-видимому следует рассматривать, как величину, содержащую глобальное время нашей Вселенной согласно формуле R3=T*C, где T - глобальное время Вселенной, а C - скорость света в вакууме или величина близкая к ней. Знак * здесь и далее означает умножить.


       Часть девятая.
       Факты, указывающие на наличие глобальной анизотропии и глобальной неоднородности Вселенной и ее пространства.

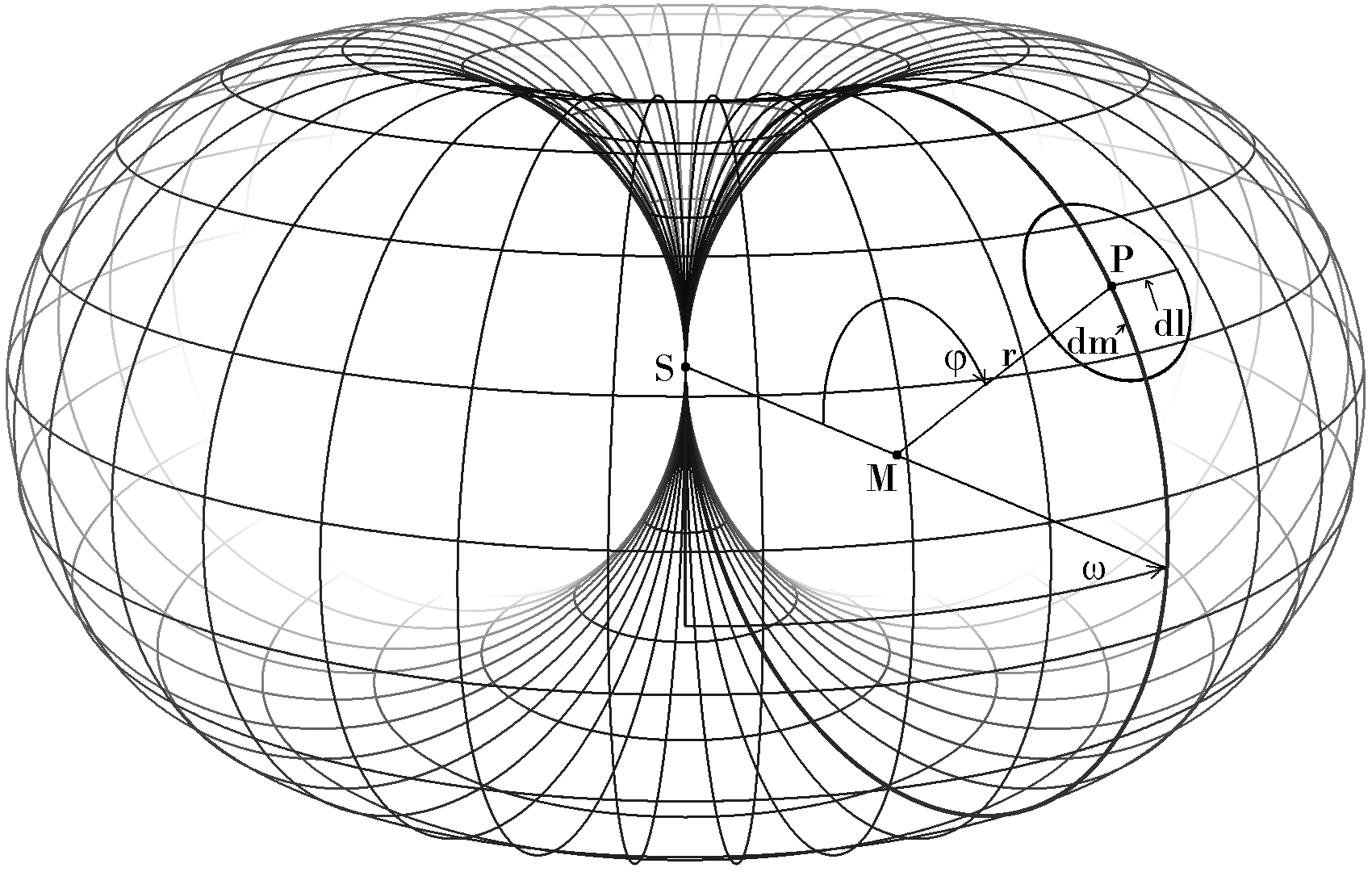
        Наиболее важным доказательством наличия глобальной анизотропии пространства Вселенной я считаю практическое отсутствие во Вселенной вещества состоящего из антиматерии (практически все вещество во Вселенной состоит из материи, а не из антиматерии). При этом ряд имеющих ненулевую массу элементарных частиц, например нейтрино, могут быть только левополяризованными, а их античастицы, в приведенном примере - антинейтрино, могут быть только правополяризованными. Подобная исключительная лево-поляризованность нейтрино, относящихся к материи, из которой состоит все вещество во Вселенной, может объясняться только наличием собственной постоянной ориентированной поляризации у Вселенной. Отсюда следует вывод о том, что глобальное пространство Вселенной имеет собственную массу и собственный момент импульса, а также еще и внутренние моменты импульса, возникающие вследствие наличия нескольких глобальных вихрей вращения тороидального типа. Аналогичный собственный момент импульса возникает, например при вращении тора вокруг его оси симметрии (на рисунке эта ось симметрии проходит через точку S). Аналогичный внутренний момент импульса возникает при вращении деформируемого вещества тора вокруг второй образующей окружности этого тора; на рисунке такой второй образующей окружностью является окружность с центром в точке M, проходящая через точки S и P. (Сама поверхность тора является фигурой вращения этой второй образующей окружности вокруг его первой образующей окружности; на рисунке такой первой образующей окружностью является окружность с центром в точке S, проходящая через точку M. При этом очевидно, что даже такое простое тело, как тор, может иметь две различных и противоположных по направлению внутренних поляризации, поскольку одному направлению вращения тора вокруг его оси симметрии, соответствует два различных направления вращения его вещества вокруг указанной его второй главной образующей окружности. Я полагаю, что вследствие наличия подобной собственной глобальной поляризации Вселенной антиматерия не может генерироваться во Вселенной в глобально больших количествах ни на какой стадии ее развития, в связи с чем мы и наблюдаем ее практическое отсутствие при сравнительно малой суммарной энергии и плотности реликтового излучения.
       В самом деле, если бы сразу после начала "Большого взрыва" материи и антиматерии во Вселенной было бы почти поровну, то после полной аннигиляции антиматерии суммарная энергия образовавшегося излучения во много раз превышала бы всю суммарную энергию всего видимого вещества во Вселенной, приведенную по формуле E=M*C*C, где M - суммарная масса всего видимого вещества во Вселенной, а С - скорость света в вакууме. Поскольку образовавшееся в результате такой аннигиляции излучение как раз и превратилось в итоге в реликтовое излучение, а образовавшиеся впоследствии черные дыры могли поглотить только незначительную его часть, то в настоящее время суммарная энергия реликтового излучения должна была бы во много раз превышать приведенную суммарную энергию всего видимого вещества во Вселенной (если бы сразу после начала "Большого взрыва" материи и антиматерии было бы почти поровну). Однако суммарная энергия реликтового излучения по современным наблюдениям ничтожную мала по сравнению с приведенной суммарной энергией всего видимого вещества во Вселенной. Следовательно, в результате "Большого взрыва" первоначально материи должно было бы возникнуть по крайней мере во много раз больше, чем антиматерии.
     Поскольку, как я полагаю, других причин практического отсутствия антиматерии во Вселенной не может быть, то отсутствие антиматерии во Вселенной является доказательством глобальной анизотропии Вселенной.

     В свою очередь, если глобальная анизотропия Вселенной будет достоверно установлена путем наблюдений, ее и следует считать причиной отсутствия антиматерии во Вселенной. В настоящее время существует довольно много исследований, подтверждающих крупномасштабную и глобальную анизотропию Вселенной. Что касается глобальной анизотропии Вселенной, то наиболее убедительные подтверждающие такую анизотропию данные получены при исследовании неоднородностей и анизотропий реликтового излучения. А именно, астрофизики обнаружили выравнивание низких мультиполей реликтового излучения вдоль так называемой "оси зла". Что же касается крупномасштабной анизотропии Вселенной, то здесь наиболее важные для нас результаты получены и опубликованы Майклом Дж. Лонго (профессор Физического факультета Мичиганского университета)в его статьях: "Есть ли у Вселенной хиральность?" 2008г. (arXiv:0812.3437v1); "Обнаружение диполя в закрученности спиральных галактик с красным смещением в диапазоне 0,04", Phisics letters B, том 699, выпуск 4, 16.05.2011г. А именно, Майклом Дж. Лонго обнаружено, что в пределах нашего сверхскопления галактик (сверхскопления Девы) и некоторых ближайших сверхскоплений наблюдается устойчивое и равномерное преобладание около 7% левосторонне закрученных галактик над правосторонне закрученными для галактик наблюдаемых в северном полушарии, относительно направления на север. Аналогичные измерения были произведены для галактик наблюдаемых в южном полушарии (М. Iye and H. Sugai, Astrophys. J. 374, 112 (1991)). Этими авторами обнаружено, что в пределах нашего сверхскопления галактик (сверхскопления Девы) и некоторых ближайших сверхскоплений наблюдается устойчивое и равномерное преобладание около 5% правосторонне закрученных галактик над левосторонне закрученными для галактик наблюдаемых в южном полушарии, относительно направления на юг. На мой взгляд и взгляд Майкла Дж. Лонго данный результат свидетельствует о наличии глобальной оси и направления закрученности Вселенной. В пользу этого вывода говорит и тот факт, что направление обнаруженной Майклом Дж. Лонго оси почти прямо противоположно направлению "холодного пятна" реликтового излучения. То есть, этот результат свидетельствует о наличии у Вселенной собственного момента импульса. Вследствие глобальной неоднородности и внутренней неравновесности Вселенной, и взаимодействия энергий ее вращения, связанных с собственным и внутренним или несколькими внутренними моментами импульса, эти различные виды ее вращения могут обладать еще и относительными прецессиями и нутациями.

       В этих условиях наиболее вероятной геометрией глобального пространства и глобального времени (с учетом глобальной анизотропии и глобальной неоднородности Вселенной) является глобальное пространство в виде сферически деформированного трехмерного гипертора (трехмерной поверхности четырехмерного гиперполнотория).
       Сразу же замечу, что эта трехмерная поверхность, большая часть поверхности которой близка к поверхности соответствующей трехмерной гиперсферы (трехмерной сферы также построенной в четырехмерном пространстве), как раз и является трехмерным пространством нашей Вселенной.


       Часть десятая.
       Алгоритм построения трехмерного тора (гипертора) в прямоугольной системе координат четырехмерного евклидова пространства. Другие виды трехмерных торов.
      
       Далее в настоящей части, я сначала буду рассматривать именно трехмерный гипертор, свободно (без применения искажающих геометрических операторов преобразований) вложенный в четырехмерное пространство, который обычно обозначается в аналитической геометрии и топологии пространств следующим образом: T3,R4, либо (T3;R4), либо T3-R4. Я буду далее пользоваться обозначением T3-R4. Здесь T3 обозначает трехмерный гипертор, который математики и физики чаще называют трехмерным тором, а R4 обозначает, что этот трехмерный гипертор является свободно вложенным в четырехмерное евклидово пространство (для нас это означает, что он может быть построен в четырехмерном евклидовом пространстве и не может быть построен в трехмерном евклидовом пространстве). Такой трехмерный гипертор является ориентируемой (иногда называют ориентированной) поверхностью, в отличие от листа Мебиуса или бутылки Клейна, и т.п., являющихся неориентированными поверхностями.
       В конце этой части я дам описание еще трех видов ориентируемого трехмерного гипертора. Один из них может быть свободно вложен в евклидово пространство с размерностью не менее 6 трехмерный тор (гипертор) Клиффорда, обозначаемый T3-R6. А два других могут быть свободно вложены в евклидово пространство с размерностью не менее 5.

       Для того, чтобы помочь неискушенному читателю разобраться в четырехмерной геометрии трехмерного гипертора, я сразу же ниже приведу ниже алгоритм его построения в четырехмерном евклидовом пространстве в прямоугольной системе координат четырех измерений.
       Такой трехмерный гипертор является ограничивающей трехмерной поверхностью соответствующего четырехмерного гиперполнотория, который в свою очередь является объемной фигурой четырехмерного пространства. Этот соответствующий четырехмерный гиперполноторий наблюдается при построении нашего трехмерного гипертора в соответствующем четырехмерном пространстве, например при его построении в четырехмерном евклидовом пространстве, в которым мы и будем его строить, переходя иногда к полярным координатам.
       Любой недеформированный трехмерный гипертор строится в четырехмерном пространстве с помощью его трех образующих окружностей, как фигура вращения. Первая образующая окружность, имеющая радиус R1, строится на двумерной евклидовой плоскости. Центр этой окружности выбирают за начало координат. В качестве первой и второй координатных осей  x1 и x2 выбираем две любые взаимно ортогональные прямые (для удобства построения используем прямоугольную систему координат), лежащие в указанной евклидовой плоскости, в которой построена указанная первая образующая окружность, и проходящих через центр этой окружности.  Для построения любой второй образующей окружности, имеющей радиус R2 одинаковый для всех таких вторых образующих окружностей, используемых для построения нашего трехмерного гипертора, необходимо трехмерное пространство, для чего к двум евклидовым координатам (осям координат) плоскости первой образующей окружности добавляем третью евклидову ось координат x3, ортогональную плоскости первой образующей окружности и проходящую через центр первой образующей окружности (для удобства построения используем прямоугольную систему координат). Далее выбираем любую плоскость полученного трехмерного евклидового пространства, проходящую через указанную третью ось координат x3, а потому ортогональную  плоскости первой образующей окружности. В этой выбранной нами плоскости, далее называемой плоскостью второй образующей окружности, строим вторую образующую окружность радиуса R2 с центром, который является одной из двух точек пересечения первой образующей окружности и этой выбранной нами плоскости (проходящей через указанную третью ось координат). Любая другая вторая образующая окружность строится аналогичным образом, как окружность с тем же радиусом R2, (что и радиус уже построенной второй образующей окружности), но лежащая в другой плоскости (построенного трехмерного евклидового пространства) проходящей через указанную третью ось координат. Таким образом, все вторые образующие окружности (какие только возможно построить подобным образом, т.е бесконечное их количество) в совокупности образуют двумерную поверхность, являющуюся двумерным тором (в построенном трехмерном евклидовом пространстве, с указанными осями координат x1, x2, x3). Эта поверхность может быть получена, как фигура вращения любой из указанных вторых образующих окружностей относительно указанной третьей координатной оси в указанном трехмерном евклидовом пространстве. Полученная таким образом двумерная поверхность, являющаяся двумерным тором, является первой образующей двумерной поверхностью (далее иногда для краткости именуемой первой образующей поверхностью) для трехмерного гипертора, который мы строим. Все точки этой  первой образующей двумерной поверхности (двумерного тора) являются центрами соответствующих третьих образующих окружностей нашего трехмерного гипертора, имеющих одинаковый радиус R3. Для построения такой третьей образующей окружности необходимо уже все указанное четырехмерное пространство построения. И поскольку мы считаем его уже выбранным, то в нем существует только одна прямая проходящая через начало координат и ортогональная всем трем остальным уже выбранным координатным осям x1, x2 и x3. Именно на этой прямой и строится координатная ось x4, имеющая общее начало координат с уже выбранными указанными координатными осями x1, x2 и x3. В качестве центра указанной третьей образующей окружности выбирается любая точка полученной первой образующей двумерной поверхности и через нее проводится ось, которая параллельна указанной четвертой координатной оси x4 (в прямоугольной системе координат) нашего четырехмерного евклидового пространства построения. Через полученную таким образом ось и прямую, на которой лежит отрезок, соединяющий указанный выбранный нами центр нашей третьей образующей окружности и центр указанной второй  образующей окружности, (второй  образующей окружности, на которой находится выбранный нами центр нашей третьей образующей окружности), проводим плоскость, далее называемую плоскостью третьей образующей окружности. (Эта плоскость третьей образующей окружности ортогональна плоскости второй образующей окружности, на которой лежит та вторая образующая окружность, на которой находится выбранный нами центр нашей третьей образующей окружности, поскольку четвертая координатная ось ортогональна указанной плоскости второй образующей окружности.) В этой полученной плоскости третьей образующей окружности строим нашу третью образующую окружность с указанными выбранным нами центром и радиусом R3. Аналогичным образом строятся все третьи образующие окружности с радиусом R3. Вся совокупность точек всех третьих образующих окружностей и образует наш построенный таким образом трехмерный гипертор. При этом наш трехмерный гипертор может быть получен с помощью любой третьей главной образующей окружности, как фигура вращения, следующим образом: Сначала выбирается любая третья главная образующая окружность. Затем с ее помощью строится вторая образующая двумерная поверхность для трехмерного гипертора, который мы строим. Эта вторая образующая двумерная поверхность является фигурой вращения этой выбранной нами третьей образующей окружности относительно оси, которая параллельна четвертой указанной координатной оси, и которая проходит через центр второй образующей окружности, на которой находится центр этой выбранной нами третьей образующей окружности; вращение при этом происходит вдоль указанной второй образующей окружности. Полученная таким образом вторая двумерная образующая поверхность является двумерным тором. (Очевидно, что эта вторая двумерная образующая поверхность построена в трехмерном пространстве, образованном плоскостью указанной (соответствующей) второй образующей окружности и указанной осью, которая параллельна четвертой указанной координатной оси). Сам же наш трехмерный гипертор может быть получен, как фигура вращения указанной полученной второй образующей двумерной поверхности (двумерного тора) вдоль первой образующей окружности, вокруг вышеуказанной третьей координатной оси (оси ортогональной плоскости первой образующей окружности и проходящей через ее центр), (впрочем как и вокруг любой оси, проходящей через начало координат, и лежащей в плоскости, образованной координатными осями x3 и x4, поскольку такая прямая ортогональна плоскости первой образующей окружности, но принадлежит выбранному четырехмерному пространству построения).
       (Для лучшего понимания геометрии четырехмерного евклидового пространства, обращаю внимание читателей на тот факт, что в евклидовом четырехмерном пространстве, в котором уже выбраны две пересекающихся ортогональных координатных оси с общим началом координат в точке их пересечения, существует бесконечное множество вариантов построения ортогональных им и друг другу координатных осей x3 и x4. А именно, плоскость, образованную осями x3 и x4, можно вращать как вокруг оси x1, так и вокруг оси x2. Аналогично в трехмерном евклидовом пространстве, в котором уже выбрана координатная ось x1, существует бесконечное множество вариантов построения ортогональных ей и друг другу координатных осей x2 и x3.  А именно, плоскость, образованную осями x2 и x3, можно вращать вокруг оси x1).
       Фактически указанная вторая двумерная образующая поверхность является половинкой сечения нашего трехмерного гипертора евклидовым трехмерным пространством, которое проходит через плоскость указанной второй образующей окружности (использованной при построении этой второй образующей двумерной поверхности) и проходит через указанную ось, которая параллельна четвертой указанной координатной оси, и которая проходит через центр этой второй образующей окружности (то есть проходит и через саму четвертую координатную ось, поскольку плоскость второй образующей  окружности проходит через начало координат). Полное же такое сечение представляет из  себя две таких вторых двумерных образующих поверхности (два таких двумерных тора), которые симметричны друг другу относительно указанной третьей оси координат и начала координат. При этом при выполнении  условия R1<R2 или R1<R2+R3 они (два таких двумерных тора) могут пересекаться друг с другом, а при выполнении условия R2<R3 они  могут быть самопересекающимися, в результате чего при построении нашего трехмерного гипертора образуются принадлежащие нашему трехмерному гипертору трехмерные поверхности дополнительных связностей, лежащие внутри другой трехмерной поверхности - трехмерной поверхности главной связности (внешней трехмерной поверхности) принадлежащей трехмерной поверхности нашего трехмерного гипертора. То есть, если выполняются условия R1<R2 или R1<R2+R3 или R2<R3 или нескольких таких условий одновременно, то каждая соответствующая третья образующая окружность будет в своей плоскости пересекаться с другими (другой) третьими образующими окружностями (в двух точках с каждой), вследствие чего у нашего трехмерного гипертора, будут образовываться одна или две, в зависимости от соотношения его трех образующих радиусов, трехмерных поверхностей дополнительной связностей, которые расположены внутри его внешней трехмерной поверхности (трехмерной поверхности главной связности), и которые сами могут пересекаться друг с другом, и могут быть самопересекающимися.
       Такой трехмерный гипертор кроме оси симметрии, являющейся указанной третьей координатной осью, имеет еще три оси симметрии, а именно оси симметрии, являющиеся соответственно первой, второй и четвертой координатной осью, что не совсем очевидно из указанного алгоритма построения, но легко проверяется, как с помощью соответствующих формул, так и методом построения соответствующих сечений с использованием вышеприведенного алгоритма построения нашего трехмерного гипертора.

       Как я уже упоминал в предыдущих частях (часть седьмая), существует еще один отдельный подвид трехмерного гипертора, вложенного в четырехмерное пространство, а именно трехмерный гипертор, у которого радиус первой образующей окружности равен нулю (R1=0). Далее такой трехмерный гипертор я буду иногда называть однократно вырожденным трехмерным гипертором (обычно его называют вырожденным трехмерным гипертором). У такого трехмерного гипертора нет первой образующей окружности, вместо такой окружности у него есть точка, лежащая в начале координат, которая и является центром для всех его вторых образующих окружностей. Первой образующей поверхностью у такого однократно вырожденного трехмерного гипертора является двумерная сфера, центр которой совпадает с началом координат, а радиус этой двумерной сферы равен R2, то есть радиусу его вторых образующих окружностей. Можно сказать, что эта двумерная сфера образована всеми (бесконечным количеством) указанных вторых образующих окружностей.

       А теперь, как и обещал вначале этой части, я дам описание еще трех видов трехмерного гипертора. Одним из этих видов является трехмерный тор (гипертор) Клиффорда. Трехмерный тор Клиффорда обозначается T3-R6, соответственно он может быть свободно вложен в шестимерное евклидово пространство и не может быть свободно вложен евклидово пространство меньшей размерности. Геометрия (топология) трехмерного тора Клиффорда отличается тем, что для каждого вида его образующих окружностей выделено по две координатных оси, которые не используются для ориентации плоскостей построения при построении образующих окружностей других видов. Если выбрать любую из точек его первой образующей окружности с радиусом R1, построенной в плоскости координатных осей x1 и x2 с центром в начале координат, то этой выбранной точке соответствует вторая образующая окружность с радиусом R2, первые две координаты x1 и x2 любой из точек которой совпадают с координатами выбранной точки первой образующей окружности. Сама же эта вторая образующая окружность имеет свой центр в этой точке (в выбранной точке первой образующей окружности) и строится в плоскости параллельной плоскости координатных осей x3 и x4. Таким же образом строятся все вторые образующие окружности, причем все их радиусы будут равны R2. То есть координаты x3 и x4, а точнее формулы связывающие эти координаты будут одинаковыми для всех вторых образующих окружностей. Аналогично, если выбрать любую из точек его второй образующей окружности, то этой выбранной точке соответствует третья образующая окружность с радиусом R3, первые четыре координаты x1, x2, x3 и x4 любой из точек которой совпадают с координатами выбранной точки второй образующей окружности. Сама же эта третья образующая окружность имеет свой центр в этой точке (в выбранной точке второй образующей окружности) и строится в плоскости параллельной плоскости координатных осей x5 и x6. Таким же образом строятся все третьи образующие окружности, причем все их радиусы будут равны R3. То есть координаты x5 и x6, а точнее формулы связывающие эти координаты будут одинаковыми для всех третьих образующих окружностей. Из этого построения ясно, что если порядок построения некоторого конкретного тора Клиффорда поменять, и сначала в качестве первой образующей окружности построить окружность c радиусом R2 (или R3), а затем в качестве второй образующей окружности построить окружность c радиусом R1 или R3 (или соответственно первой образующей окружности с радиусом R3 построить окружность c радиусом R1 или R2), а затем в качестве третьей образующей окружности построить окружность c оставшимся еще не использованным радиусом, так, чтобы все три радиуса были разными, то все равно получится тот же самый - такой же по форме и размерам тор Клиффорда, поменяется лишь его ориентация в осях координат, поскольку изменится последовательность использования координатных осей. Дело в том, что наборы пар координат, соответствующих каждому виду образующей окружности, для каждой топологически эквивалентной точки всех результирующих торов Клиффорда останутся неизменными при таком изменении порядка построения тора Клиффорда. То есть построение тора Клиффорда является коммутативным (перестановочным) в отношении порядка использования, то есть перестановки  номеров , его образующих окружностей. Следовательно, трехмерный тор Клиффорда является простым декартовым произведением, иначе называемым прямым произведением, его трех образующих окружностей. Коммутативность здесь проявляется в том, что результат (в смысле формы и размеров результата) не зависит от порядка расположения сомножителей, что выражается следующей формулой:

       (T3-R6)=(S1-R2)(1)*(S1-R2)(2)*(S1-R2)(3)= (S1-R2)(1)*(S1-R2)(3)*(S1-R2)(2)= (S1-R2)(2)*(S1-R2)(1)*(S1-R2)(3)= (S1-R2)(2)*(S1-R2)(3)*(S1-R2)(1)= (S1-R2)(3)*(S1-R2)(1)*(S1-R2)(2)= (S1-R2)(3)*(S1-R2)(2)*(S1-R2)(1)
       Здесь: (S1-R2)(1) - обозначение первой образующей окружности;
       (S1-R2)(2) - обозначение второй образующей окружности;
       (S1-R2)(3) - обозначение третьей образующей окружности.
       Обозначение S1-R2 означает одномерную сферу (окружность) свободно вписанную в двумерное пространство.
       При таком прямом произведении складываются как размерности перемножаемых поверхностей, так и размерности, пространств, в которые они вложены.

       В аналитической геометрии и топологии обычно сам порядок построения определяется через определение прямого произведения, но здесь это увело бы нас в достаточно непростую область теории множеств. Поэтому здесь нам удобнее наоборот продемонстрировать чем же является прямое произведение на примере соответствующего построения. Коммутативность и соответствующая неизменность результирующих координатных наборов, состоящих из неизменных наборов координат точек сомножителей, являются основными свойствами и по сути определением прямого произведения любых поверхностей и объемных геометрических фигур.
       
       Трехмерный тор Клиффорда является максимально симметричным из всех видов трехмерных торов. Трехмерный тор Клиффорда, все образующие окружности которого имет радиус 1, может быть свободно вписан в шестимерную гиперсферу радиуса равного корню квадратному из 3. Вероятно именно поэтому в аналитической геометрии и топологии трехмерный тор Клиффорда также часто называют кубическим тором. Как я уже упоминал во введении к настоящей статье, для космической топологии трехмерный тор Клиффорда интересен тем, что сумма углов любого вписанного в него треугольника равна 180 градусов. Будучи пространственно разрезанным поперек всех его образующих окружностей, такой разрезанный тор Клиффорда при выпрямлении всех его образующих окружностей свободно неискаженно накладывается на трехмерное евклидово пространство, так же, как аналогично разрезанный поперек всех своих окружностей цилиндр или конус свободно неискаженно накладывается на евклидову плоскость. Если же такому разрезу строго перпендикулярно образующим окружностям и последующему выпрямлению всех его образующих окружностей подвергнуть трехмерный тор Клиффорда, все образующие окружности которого имет радиус 1, то мы получим трехмерный куб с длиной каждого ребра равной 1, который свободно неискаженно накладывается на трехмерное евклидово пространство.

       Еще один вид трехмерного гипертора (трехмерного тора), я назвал трехмерным смешанным тором Клиффорда. Юмора ради я назвал его также трехмерным тором Левичева-Клиффорда, поскольку не нашел в литературе его описания. Это конечно не претензия, и я буду благодарен, если кто-то подскажет мне уже имеющееся в литературе его описание и название. Трехмерный смешанный тор Клиффорда обозначается T3-R5-1, соответственно он может быть свободно вложен в пятимерное евклидово пространство и не может быть свободно вложен евклидово пространство меньшей размерности.
       У трехмерного смешанного тора Клиффорда, первые две образующие окружности строятся также, как и для двумерного или трехмерного тора Клиффорда. Его первой образующей поверхностью является двумерный тор Клиффорда. А его третьи образующие окружности строятся с использованием вторых образующих окружностей и пятой координатной оси также, как строятся третьи образующие окружности трехмерного тора (гипертора) T3-R4 (вложенного в четырехмерное пространство), но вместо четвертой координатной оси (уже занятой) используется пятая координатная ось. Такой смешанный тор Клиффорда  (тор T3-R5-1) является прямым произведением окружности S1-R2 и двумерного тора свободно вложенного в трехмерное пространство T2-R3 (обычного двумерного тора). Поскольку прямое произведение коммутативно, то и порядок построения смешанного тора Клиффорда может быть соответствующим образом изменен:

       (T3-R5-1)=(S1-R2)*(T2-R3)=(T2-R3)*(S1-R2)

        Оставшимся видом трехмерного тора является сферический трехмерный тор Клиффорда. У сферического трехмерного тора Клиффорда, который обозначается T3-R5-2, первой образующей двумерной поверхностью является двумерная сфера. А его третьи образующие окружности строятся с использованием первой образующей двумерной поверхности (или вторых образующих окружностей) и четвертой и пятой координатных осей также, как строятся третьи образующие окружности трехмерного тора Клиффорда (трехмерного тора T3-R6 вложенного в шестимерное пространство) с использованием  пятой и шестой координатных осей. Такой сферический трехмерный тор Клиффорда (тор T3-R5-2) является прямым произведением двумерного сферы свободно вложенной в трехмерное пространство S2-R3 (обычной двумерной сферы) и окружности S1-R2. Поскольку прямое произведение коммутативно, то и порядок построения сферического тора Клиффорда может быть соответствующим образом изменен:

       (T3-R5-2)=(S2-R3)*(S1-R2)=(S1-R2)*(S2-R3)

       Поскольку двумерная сфера является вырожденным двумерным тором, то есть двумерным тором, у которого радиус первой образующей окружности равен нулю, то сферический трехмерный тор Клиффорда T3-R5-2 можно рассматривать, как частный случай (подвид) смешанного тора Клиффорда T3-R5-1.

      
       Многомерные смешанные торы Клиффорда (торы Левичева-Клиффорда).
       Все смешанные торы Клиффорда могут быть представлены в виде прямых произведений одной или нескольких сфер любых размерностей (в том числе размерности 1, т.е. окружностей) и одного или нескольких (обычных) торов (TM-R(M+1)) любых размерностей от 2 и более, вложенных в пространство с размерностью большей на 1, чем их собственная размерность. Для отличия его обозначения от торов других классов к его обозначению добавляется в конце -1 единица через дефис.
       Например, прямое произведение двух окружностей S1-R2 и одного двумерного тора T2-R3 (обычного двумерного тора) образует четырехмерный смешанный тор Клиффорда, вложенный в семимерное пространство. Поскольку прямое произведение коммутативно, то и порядок построения смешанного тора Клиффорда может быть соответствующим образом изменен:

       (T4-R7-1)=(S1-R2)(1)*(S1-R2)(2)*(T2-R3)= (S1-R2)(1)*(T2-R3)*(S1-R2)(2)= (T2-R3)*(S1-R2)(1)*(S1-R2)(2)=(S1-R2)(2)*(S1-R2)(1)*(T2-R3)= (S1-R2)(2)*(T2-R3)*(S1-R2)(1)= (T2-R3)*(S1-R2)(2)*(S1-R2)(1) 
 
       А, прямое произведение одной окружности S1-R2 и  и одного трехмерного тора T3-R4 образуют четырехмерный смешанный тор Клиффорда, вложенный в шестимерное пространство:

       (T4-R6-1)=(S1-R2)*(T3-R4)=(T3-R4)*(S1-R2)

       Соответственно, прямое произведение одной окружности S1-R2, одного двумерного тора T2-R3 (обычного двумерного тора) и одного трехмерного тора T3-R4 (обычного трехмерного тора) образует шестимерный смешанный тор Клиффорда, вложенный в девятимерное пространство T6-R9-1.

       Поскольку смешанные торы Клиффорда заданной размерности и заданной размерности содержащего их пространства для больших размерностей могут быть построены с помощью неодинаковых наборов видов сомножителей, то для идентификации их вида в общем случае необходимо использовать формулу его построения. Например, сочетания двух видов сомножителей:
T2-R3 (обычный двумерный тор) и T4-R5 (четырехмерный тор) дают тот же вклад в размерность результирующего смешанного тора Клиффорда и размерность пространства, в которое он свободно вложен, что и сочетания двух других видов сомножителей: T3-R4 (трехмерный тор) и T3-R4 (трехмерный тор). Таким образом, смешанные торы Клиффорда (T7-R10-1)=(S1-R2)*(T2-R3)*(T4-R5) и (T7-R10-1)=(S1-R2)*(T3-R4)*(T3-R4) это разные виды торов.

      
       Многомерные сферические торы Клиффорда.
       Сферическим тором Клиффорда является прямое произведение двух или более сфер любых размерностей, хотя бы одна из которых имеет размерность более 1, то есть является не окружностью, а двумерной, или трехмерной, или сферой большей размерности. Для отличия его обозначения от торов других классов к его обозначению добавляется в конце -2 двойка через дефис. Поскольку многомерные сферические торы Клиффорда заданной размерности и заданной размерности содержащего их пространства могут быть построены с помощью неодинаковых наборов видов сомножителей, то для идентификации вида сферического тора Клиффорда в общем случае необходимо использовать формулу его построения. Например, сочетания двух видов сомножителей:
S1-R2 (окружность- одномерная сфера) и S3-R4 (трехмерная сфера) дают тот же вклад в размерность результирующего сферического тора Клиффорда, что и сочетания двух других видов сомножителей: S2-R3 (двумерная сфера) и S2-R3 (двумерная сфера). Таким образом, сферические торы Клиффорда (T4-R6-2)=(S1-R2)*(S3-R4) и (T4-R6-2)=(S2-R3)*(S2-R3) это разные виды торов.

       Поскольку N-мерная сфера является полностью вырожденным N-мерным тором (тором у которого радиусы всех образующих окружностей, кроме N-ой, равны нулю, то класс сферических торов Клиффорда можно рассматривать, как подкласс класса смешанных торов Клиффорда.

       Многомерные торированные торы Клиффорда.
       Торированным тором Клиффорда является прямое произведение одного или нескольких (обычных) торов (TM-R(M+1)) любых размерностей от 2 и более, вложенных в пространство с размерностью большей на 1, чем их собственная размерность. Для отличия его обозначения от торов других классов к его обозначению добавляется в конце -3 тройка через дефис. Например,  торированный тор Клиффорда, являющийся прямым произведением двух двумерных торов T2-R3, обозначается следующим образом: T4-R6-3.
        Поскольку многомерные торированные торы Клиффорда заданной размерности и заданной размерности содержащего их пространства для больших размерностей могут быть построены с помощью неодинаковых наборов видов сомножителей, то для идентификации вида торированного тора Клиффорда в общем случае необходимо использовать формулу его построения. Например, сочетания двух видов сомножителей:
T2-R3 (обычный двумерный тор) и T4-R5 (четырехмерный тор) дают тот же вклад в размерность результирующего  торированного тора Клиффорда, что и сочетания двух других видов сомножителей: T3-R4 (трехмерный тор) и T3-R4 (трехмерный тор). Таким образом,  торированного  торы Клиффорда (T6-R8-3)=(T2-R3)*(T4-R5) и (T6-R8-3)=(T3-R4)*(T3-R4) это разные виды торов.


       Обобщенные торы Клиффорда.
       Все вышеперечисленные классы торов относятся к одному типу торов, называемому обобщенными торами Клиффорда.
       Обобщенным тором Клиффорда является прямое произведение двух или более ориентированных поверхностей, каждая из которых является одной из следующего списка поверхностей: сферы любых размерностей, включая 1 (окружности); обычные торы (то есть торы свободно вложенные в пространство с размерностью большей на 1, чем их собственная размерность) с размерностью от 2 и выше.
 
       Заметим, что в общем случае, для всех указанных классов и типов торов, для получения соответствующих элипсоидных торов, окружности могут быть заменены на эллипсы, сферы любых размерностей на эллипсоиды тех же размерностей, а обычные торы  (TM-R(M+1)) любых размерностей от 2 и более (вложенные в пространство с размерностью большей на 1, чем их собственная размерность), на обычные элипсоидные торы тех же размерностей.   
      
      
       Экзотические торы Клиффорда - отдельный тип торов.

       Экзотическим тором Клиффорда будем называть прямое произведение одной или более неориентируемых поверхностей любых размерностей, минимального рода (сдвоенные, строенные и.т.д. поверхности исключаются, так как в результате получаются уже не торы, а восьмерки, брецели, и т.п., соответствующих размерностей), хотя бы одна из которых имеет размерность более 1, например проективная плоскость, бутылка Клейна, и.т.д., а также одной или нескольких из следующих ориентированных поверхностей: сфер любых размерностей, в т.ч. 1; обычных торов (TM-R(M+1)) любых размерностей от 2 и более, вложенных в пространство с размерностью большей на 1, чем их собственная размерность. 


       Часть одиннадцатая.
       Формула трехмерного гипертора в прямоугольной системе координат четырехмерного евклидова пространства.

       Как и в предыдущей части полагаем, что центр первой образующей окружности совмещен с началом координат и первая образующая окружность лежит в плоскости, образованной координатными осями x1 и x2 (при x3=0 и x4=0), а вторые образующие окружности лежат в плоскостях ортогональных плоскости, образованной координатными осями x1 и x2, но в пространстве образованном координатными осями x1, x2 и x3 (при x4=0)

       Формулы тора и трехмерного гипертора.

       Формулы тора:
       В трехмерном евклидовом пространстве система уравнений для тора, являющегося двумерной поверхностью, задается в параметрическом виде, то есть в виде зависимостей евклидовых ("плоских") прямоугольных координат (x1,x2,x3) каждой точки тора от соответствующих (этим точкам) углов (параметров) при заданном радиусе R первой образующей окружности и заданном радиусе r второй образующей окружности, согласно следующих формул:

       x1(угол фи, угол омега)={R+r*cos(угол фи)}*cos(угол омега)
       x2(угол фи, угол омега)={R+r*cos(угол фи)}*sin(угол омега)
       x3(угол фи, угол омега)=r*sin(угол фи)

       Здесь:
       R - радиус первой образующей окружности;
       r - радиус второй образующей окружности;
       угол фи - угол между следующими двумя лучами (половинками прямых): первый луч - луч, соединяющий описываемую точку поверхности тора и центр второй образующей окружности, соответствующей этой точке, (и исходящий из этого центра)(на рисунке это луч исходящий из точки M и проходящий через точку P); второй луч - луч, исходящий из центра указанной первой образующей окружности и проходящий через центр второй образующей окружности (на рисунке это луч исходящий из точки S и проходящий через точку M); этот угол фи равен угол пи минус угол фи на рисунке;
       угол омега - угол между следующими двумя лучами (половинками прямых): первый луч - луч, исходящий из центра первой образующей окружности и проходящий через центр указанной второй образующей окружности; второй луч - положительная часть координатной оси x1.

       Для дальнейшего анализа полезно перейти к обозначениям в универсальных тороидальных координатах. Уравнения тора в универсальных координатах:

       x1(уг.фи1, уг.фи2)={R+r*cos(уг.фи2)}*cos(уг.фи1)
       x2(уг.фи1, уг.фи2)={R+r*cos(уг.фи2)}*sin(уг.фи1)
       x3(уг.фи1, уг.фи2)=r*sin(уг.фи2)

       Здесь:
       R1 - радиус первой образующей окружности;
       R2 - радиус второй образующей окружности;
       угол фи2 (сокращенное обозначение - уг.фи2) - угол между следующими двумя лучами (половинками прямых): первый луч - это луч, проходящий через описываемую точку поверхности тора и исходящий из центра второй образующей окружности, соответствующей этой описываемой точке (на рисунке это луч исходящий из точки M и проходящий через точку P); второй луч - луч, исходящий из центра указанной первой образующей окружности и проходящий через центр второй образующей окружности (на рисунке это луч исходящий из точки S и проходящий через точку M); этот уг.фи2 равен угол пи (сокращенно уг.пи) минус угол фи (сокращенно уг.фи) на рисунке (уг.фи2)=(уг.пи-уг.фи), где уг.пи=3,14 радиан;
       уг.фи1 - угол между следующими двумя лучами (половинками прямых): первый луч - луч, исходящий из центра первой образующей окружности и проходящий через центр указанной второй образующей окружности; второй луч - положительная часть координатной оси x1.

       Формулы трехмерного гипертора (трехмерного тора T3-R4):
      
       В четырехмерном евклидовом пространстве формулы для трехмерного гипертора (трехмерного тора T3-R4), являющегося трехмерной поверхностью, задаются в параметрическом виде, а именно в виде зависимостей евклидовых ("плоских") прямоугольных координат (x1,x2,x3,x4) каждой точки трехмерного гипертора от соответствующих (этим точкам) углов (параметров) при заданных радиусах образующих окружностей (R1,R2,R3).
       Уравнения трехмерного гипертора в универсальных тороидальных координатах:

   x1(уг.фи1, уг.фи2, уг.фи3)={R1+[R2+R3*cos(уг.фи3)]*cos(уг.фи2)}*cos(уг.фи1)
   x2(уг.фи1, уг.фи2, уг.фи3)={R1+[R2+R3*cos(уг.фи3)]*cos(уг.фи2)}*sin(уг.фи1)
   x3(уг.фи1, уг.фи2, уг.фи3)=[R2+R3*cos(уг.фи3)]*sin(уг.фи2)
   x4(уг.фи1, уг.фи2, уг.фи3)=R3*sin(уг.фи3)

         Здесь:
       R1 - радиус первой образующей окружности;
       R2 - радиус второй образующей окружности;
       R3 - радиус третьей образующей окружности;
       угол фи3 (сокращенное обозначение - уг.фи3 или у.фи3) - угол между следующими двумя лучами (половинками прямых): первый луч - это луч, проходящий через описываемую точку трехмерной поверхности гипертора и исходящий из центра третьей образующей окружности, соответствующей этой описываемой точке; второй луч - это луч, исходящий из центра указанной второй образующей окружности и проходящий через центр соответствующей третьей образующей окружности;
       угол фи2 (сокращенное обозначение - уг.фи2 или у.фи2) - угол между следующими двумя лучами (половинками прямых): первый луч - луч, исходящий из центра указанной второй образующей окружности и проходящий через центр указанной третьей образующей окружности (если считать, что изображенный на рисунке тор это первая образующая поверхность, то на рисунке это луч исходящий из точки M и проходящий через точку P); второй луч - луч, исходящий из центра указанной первой образующей окружности и проходящий через центр второй образующей окружности (если считать, что изображенный на рисунке тор это первая образующая поверхность, то на рисунке это луч исходящий из точки S и проходящий через точку M);
       угол фи1 (сокращенное обозначение - уг.фи1 или у.фи1) - угол между следующими двумя лучами (половинками прямых): первый луч - луч, исходящий из центра первой образующей окружности и проходящий через центр указанной второй образующей окружности; второй луч - положительная часть координатной оси x1.


       Формулы N-мерного (многомерного) гипертора (N-мерного (многомерного) тора TN-R(N+1)):
      
       В (N+1)-мерном евклидовом пространстве формулы для N-мерного гипертора (N-мерного тора TN-R(N+1)), являющегося N-мерной поверхностью, задаются в параметрическом виде, а именно в виде зависимостей евклидовых ("плоских") прямоугольных координат (x1,x2,x3,x4,...,xN,x(N+1)) каждой точки N-мерного гипертора от соответствующих (этим точкам) углов (параметров) при заданных радиусах образующих окружностей (R1,R2,R3,...,R(N-1),RN).
       Уравнения N-мерного гипертора в универсальных тороидальных координатах:

  x1(у.фи1, у.фи2, у.фи3,...,у.фи(N-1), у.фиN)=
  ={R1+[R2+[R3... +[R(N-1)+RN*cos(у.фиN)]*cos(у.фи(N-1))* ...]*cos(у.фи3)]*cos(у.фи2)}*cos(у.фи1)
  x2(у.фи1, у.фи2, у.фи3,...,у.фи(N-1), у.фиN)=
  ={R1+[R2+[R3... +[R(N-1)+RN*cos(у.фиN)]*cos(у.фи(N-1))* ...]*cos(у.фи3)]*cos(у.фи2)}*sin(у.фи1)
  x3(у.фи1, у.фи2, у.фи3,...,у.фи(N-1), у.фиN)=
  ={R2+[R3+... +[R(N-1)+RN*cos(у.фиN)]*cos(у.фи(N-1))* ...]*cos(у.фи3)}*sin(у.фи2)
  ...................... ............................. ..................... ..................... ........................
  x(N-1)(у.фи1, у.фи2, у.фи3,..,у.фи(N-1),у.фиN) ={R(N-2)+[R(N-1) +RN*cos(у.фиN)]*cos(у.фи(N-1)}*sin(у.фи(N-2))
  xN(у.фи1, у.фи2, у.фи3,.......,у.фи(N-1), у.фиN) =[R(N-1)+RN*cos(у.фиN)]*sin(у.фи(N-1))
  x(N+1)(у.фи1, у.фи2, у.фи3,..,у.фи(N-1),у.фиN) =RN*sin(у.фиN)
 
       Здесь:
       R1 - радиус первой образующей окружности;
       R2 - радиус второй образующей окружности;
       R3 - радиус третьей образующей окружности;
       ...................... ............................. ..................... ..................... ........................
       R(N-1) - радиус N-1 образующей окружности;
       RN - радиус N образующей окружности;
       угол фиN (сокращенное обозначение - уг.фиN или у.фиN) - угол между следующими двумя лучами (половинками прямых): первый луч - это луч, проходящий через описываемую точку N-мерной поверхности гипертора и исходящий из центра N образующей окружности, соответствующей этой описываемой точке; второй луч - это луч, исходящий из центра указанной N-1 образующей окружности и проходящий через центр соответствующей N образующей окружности;
      ...................... ............................. ..................... ..................... ........................
       угол фи3 (сокращенное обозначение - уг.фи3 или у.фи3) - угол между следующими двумя лучами (половинками прямых): первый луч - это луч, проходящий через описываемую точку трехмерной поверхности гипертора и исходящий из центра третьей образующей окружности, соответствующей этой описываемой точке; второй луч - это луч, исходящий из центра указанной второй образующей окружности и проходящий через центр соответствующей третьей образующей окружности;
       угол фи2 (сокращенное обозначение - уг.фи2 или у.фи2) - угол между следующими двумя лучами (половинками прямых): первый луч - луч, исходящий из центра указанной второй образующей окружности и проходящий через центр указанной третьей образующей окружности (если считать, что изображенный на рисунке тор это первая образующая поверхность, то на рисунке это луч исходящий из точки M и проходящий через точку P); второй луч - луч, исходящий из центра указанной первой образующей окружности и проходящий через центр второй образующей окружности (если считать, что изображенный на рисунке тор это первая образующая поверхность, то на рисунке это луч исходящий из точки S и проходящий через точку M);
       угол фи1 (сокращенное обозначение - уг.фи1 или у.фи1) - угол между следующими двумя лучами (половинками прямых): первый луч - луч, исходящий из центра первой образующей окружности и проходящий через центр указанной второй образующей окружности; второй луч - положительная часть координатной оси x1.


      
       Часть двенадцатая.
       Формулы апроксимации трехмерного гипертора (трехмерного тора T3-R4) трехмерной гиперсферой (трехмерной сферой S3-R4) для
       случая, когда  R1<<R3 и R2<<R3.
       Прежде, чем приступить к указанной апроксимации, полезно в формулах трехмерного гипертора выделить часть, соответствующую описанию трехмерной гиперсферы. Для этого вышеприведенные (в предыдущей части) формулы трехмерного гипертора переписаны ниже в виде линейных от  R1, R2 и R3 уравнений. Если в правой части этих нижеследующих формул оставить только слагаемые содержащие R3, (заключенные в квадратные скобки), мы получим уравнения (систему уравнений) трехмерной гиперсферы с радиусом равным R3 в виде уравнений связывающих евклидовы координаты (x1,x2,x3,x4) трехмерной гиперсферы с универсальными тороидальными координатами, (что легко проверить, убедившись в том, что сумма квадратов x1,x2,x3 и x4, в левой части уравнений равна R3*R3). Если же сделать наоборот, то есть в правой части нижеследующих формул исключить только часть, заключенную в квадратные скобки, и оставить только слагаемые, содержащие  R1 и R2, мы получим уравнения двумерного тора с радиусом первой образующей окружности равным R1 и радиусом второй образующей окружности равным R2; причем этот  двумерный тор является первой образующей двумерной поверхностью для описываемого трехмерного гипертора (трехмерного тора T3-R4). Полезно также отметить, что если в правой части нижеследующих формул оставить только слагаемые содержащие R2, мы получим уравнения (систему уравнений) двумерной сферы с радиусом равным R2, а если там оставить только слагаемые содержащие R1, мы получим уравнения (систему уравнений) окружности с радиусом равным R1, являющейся первой образующей окружностью.

 x1(у.фи1,у.фи2,у.фи3)= [R3*cos(у.фи3)*cos(у.фи2)*cos(у.фи1)] +R2*cos(у.фи2)*cos(у.фи1)+R1*cos(у.фи1)

 x2(у.фи1,у.фи2,у.фи3)= [R3*cos(у.фи3)*cos(у.фи2)*sin(у.фи1)] +R2*cos(у.фи2)*sin(у.фи1)+R1*sin(у.фи1)

 x3(уг.фи1,уг.фи2,уг.фи3)= [R3*cos(уг.фи3)*sin(уг.фи2)] +R2*sin(уг.фи2)
 
 x4(уг.фи1,уг.фи2,уг.фи3)=[R3*sin(уг.фи3)]

       Аналогичным образом и в формулах для N-мерного (многомерного) тора TN-R(N+1) можно выделить часть, описывающую N-мерную сферу SN-R(N+1) в тороидальных координатах, для этого в правой части формул оставить только слагаемые, содержащие RN. Если наоборот, исключить из этих формул только слагаемые, содержащие RN, то мы получим уравнения (систему уравнений), описывающую первую образующую (N-1)-мерную поверхность. Если исключить из этих формул только слагаемые, содержащие RN и R(N-1), то мы получим уравнения (систему уравнений), описывающую первую образующую (N-2)-мерную поверхность, и так далее. Если в правой части этих формул оставить только слагаемые содержащие R(N-1), мы получим уравнения (систему уравнений) (N-1)-мерной сферы с радиусом равным R(N-1), а если там оставить только слагаемые содержащие R(N-2), мы получим уравнения (систему уравнений) окружности с радиусом равным R(N-2), и так далее.

       Очевидно, что когда выполняются условия R1<<R3 и R2<<R3, то формулы трехмерного гипертора, приведенные в предыдущей главе, в определенном диапазоне углов аппроксимируются следующими формулами описывающими в четырехмерном евклидовом пространстве трехмерную гиперсферу через используемые тороидальные координаты:

    x1(уг.фи1, уг.фи2, уг.фи3)= R3*cos(уг.фи3)*cos(уг.фи2)*cos(уг.фи1)
    x2(уг.фи1, уг.фи2, уг.фи3)= R3*cos(уг.фи3)*cos(уг.фи2)*sin(уг.фи1)
    x3(уг.фи1, уг.фи2, уг.фи3)= R3*cos(уг.фи3)*sin(уг.фи2)
    x4(уг.фи1, уг.фи2, уг.фи3)= R3*sin(уг.фи3)

       Очевидно, что эта аппроксимация является некорректной для некоторых углов фи2 и фи3. Из вышеприведенных формул следуют условия, накладываемые на углы для корректности (допустимости) аппроксимации (при выполнении условий R1<<R3 и R2<<R3):
       cos(уг.фи3)>>R2/R3
       cos(уг.фи2)>>R1/(R3*cos(уг.фи3))


       Аналогичная аппроксимация N-мерного тора TN-R(N+1)) N-мерной сферой SN-R(N+1) также допустима при аналогичных условиях: R1<<RN, R2<<RN,...,R(N-1)<<RN,
       cos(уг.фиN)>>R(N-1)/RN
       cos(уг.фи(N-1))>>R(N-1)/(RN*cos(уг.фиN))
       ...................... ............................. ..................... ..................... ........................
       cos(уг.фи2)>>R1/(RN*cos(уг.фиN))
      

       Следует также учитывать тот факт, что при выполнении условий R1<R3 и R2<R3, соответствующий трехмерный гипертор (трехмерный тор T3-R4) получается самопересекающимся. Если при этом R1 не равно R2, то такой самопересекающийся трехмерный гипертор является четырехслойным. А в случае R1=R2 имеет место частичное вырождение, с местной накладкой двух внутренних слоев и образованием местной трехслойности при  x3=0 (уг.фи3=0). При x4=0, x3=0 расстояния между его ближайшими друг к другу (соседними) четырьмя слоями пространства, в направлении радиус вектора с началом в начале координат, будут равны соответственно в последовательности удаления от начала координат: 2R1, 2(R2-R1), 2R1, при условии R2>R1; либо 2R2, 2(R1-R2), 2R2, при условии R1>R2.
       А более точно, при выполнении условий R1<<R3 и R2<<R3, вплоть до точек самопересечения и при выполнении условий cos(уг.фи3)>R2/R3 и cos(уг.фи2)>R1/(R3*cos(уг.фи3)), для всех возможных x3 и x4, расстояния между этими его слоями будут равны (с точность до слагаемых порядка R1 и R2, пренебрегая слагаемыми порядка (R1*R1)/R3, (R2*R2)/R3, (R1*R2)/R3 и меньшими) соответственно:
       при условии R2>R1 или R2=R1
       2R1*cos(уг.фи3)*cos(уг.фи2),
       2R2*cos(уг.фи3)-2R1*cos(уг.фи3)*cos(уг.фи2),
       2R1*cos(уг.фи3)*cos(уг.фи2);

       при условии R1>R2
       2R2*cos(уг.фи3),
       2R1*cos(уг.фи3)*cos(уг.фи2)-2R2*cos(уг.фи3),
       2R2*cos(уг.фи3).

       Такой самопересекающийся трехмерный гипертор имеет следующие области самопересечения:
       во-первых, две окружности радиуса R1, заданных формулами (системой уравнений):
       (x2*x2)+(x1*x1)=R1*R1,
       x3=0, x4=R3-R2*R2/R3,    (приблизительно),
       x3=0, x4= -(R3-R2*R2/R3) (приблизительно);
      
       во-вторых, две деформированные окружности (два эллипса) с центром в начале координат и радиусами приблизительно равными соответственно:
 
  при условии R2>R1 или R2=R1
  R3+R2*cos(уг.фи3)-(R2*R2/R3)-(R1*R1/R3) и R3+R2*cos(уг.фи3)-(R2*R2/R3)+(R1*R1/R3), лежащие в плоскости координатных осей x3 и x4, определяемые формулами (системой уравнений):
  x1=0, x2=0, (то есть в плоскости координатных осей x3 и x4, то есть когда cos(уг.фи3)=sin(уг.фи2))
 (x3*x3)+(x4*x4)=(R3+R2*cos(уг.фи3)- (R2*R2/R3)-(R1*R1/R3))* (R3+R2*cos(уг.фи3)- (R2*R2/R3)-(R1*R1/R3)),
 (x3*x3)+(x4*x4)=(R3+R2*cos(уг.фи3)- (R2*R2/R3)+(R1*R1/R3))*(R3+R2*cos(уг.фи3)- (R2*R2/R3)+(R1*R1/R3));

  при условии R2<R1
  R3+R2*cos(уг.фи3)-(R1*R1/R3)-(R2*R2/R3) и R3+R2*cos(уг.фи3))-(R1*R1/R3)+(R2*R2/R3), лежащие в плоскости координатных осей x3 и x4, определяемые формулами (системой уравнений):
  x1=0, x2=0, (то есть в плоскости координатных осей x3 и x4, то есть когда cos(уг.фи3)=sin(уг.фи2))
 (x3*x3)+(x4*x4)=(R3+R2*cos(уг.фи3)- (R1*R1/R3)-(R2*R2/R3))* (R3+R2*cos(уг.фи3)- (R1*R1/R3)-(R2*R2/R3)),
 (x3*x3)+(x4*x4)=(R3+R2*cos(уг.фи3)- (R1*R1/R3)+(R2*R2/R3))* (R3+R2*cos(уг.фи3)- (R1*R1/R3)+(R2*R2/R3));

       в-третьих, деформированный (эллипсоидный) двумерный тор, заданный формулами (системой уравнений):
  (x3*x3)+(x4*x4)=(R3+R2*cos(уг.фи3) -(R1*R1/R3))*(R3+R2*cos(уг.фи3) -(R1*R1/R3))
  (x2*x2)+(x1*x1)=R2*R2;

         в-четвертых, при условии R2=R1 появляется еще одна область самопересечения -  правильная сфера радиуса R3, определяемая формулами (системой уравнений):
   x3=0,
   (x1*x1)+(x2*x2)+(x4*x4)=R3*R3.

       Если построить сечения этого трехмерного гипертора трехмерным пространством, образованном четвертой координатной осью, третьей координатной осью и любой осью, лежащей в плоскости, образованной первой и второй координатной осью, мы получим два пересекающихся самопересекающихся двумерных тора. Расстояние между центрами симметрии этих двумерных торов  равно 2R1; (также и расстояние между их осями симметрии параллельными четвертой координатной оси x4 равно 2R1; также и расстояние между их осями симметрии параллельными третьей координатной оси x3 равно 2R1).

       Поэтому, строго говоря, рассматриваемый трехмерный гипертор, при выполнении условий R1<<R3 и R2<<R3, в указанной области углов аппроксимируется четырьмя вложенными друг в друга деформированными трехмерными гиперсферами переменных радиусов, и эти радиусы близки к R3 и различаются между такими соседними гиперсферами на следующие величины:
       при условии R2>R1 или R2=R1
       2R1*cos(уг.фи3)*cos(уг.фи2);
       2R2*cos(уг.фи3)-2R1*cos(уг.фи3)*cos(уг.фи2);
       2R1*cos(уг.фи3)*cos(уг.фи2),
       и равны соответственно начиная от внешней гиперсферы:
      
       R3+R2*cos(уг.фи3)+R1*cos(уг.фи3)*cos(уг.фи2);
       R3+R2*cos(уг.фи3)-R1*cos(уг.фи3)*cos(уг.фи2);
       R3-R2*cos(уг.фи3)+R1*cos(уг.фи3)*cos(уг.фи2);
       R3-R2*cos(уг.фи3)-R1*cos(уг.фи3)*cos(уг.фи2);

       при условии R1>R2
       2R2*cos(уг.фи3),
       2R1*cos(уг.фи3)*cos(уг.фи2)-2R2*cos(уг.фи3),
       2R2*cos(уг.фи3)

       и равны соответственно начиная от внешней гиперсферы:
      
       R3+R2*cos(уг.фи3)+R1*cos(уг.фи3)*cos(уг.фи2);
       R3-R2*cos(уг.фи3)+R1*cos(уг.фи3)*cos(уг.фи2);
       R3+R2*cos(уг.фи3)-R1*cos(уг.фи3)*cos(уг.фи2);
       R3-R2*cos(уг.фи3)-R1*cos(уг.фи3)*cos(уг.фи2);
      
       Данный тип расслоения гипертора, в частности трехмерного гипертора, я предлагаю назвать гиперсферическим расслоением.

       В соответствующих полярных координатах, где углы для радиус-вектора описываемой точки отсчитываются от направлений соответствующих координатных осей x2; x3; x4, и обозначаются соответственно Фи1; Фи2; Фи3, где (Фи3=(1/2)*пи-фи3) и (Фи2=(1/2)*пи-фи2), Фи1=фи1,   указанные формулы трехмерного гипертора аппроксимируются следующими формулами трехмерной гиперсферы:

    x1(Фи1, Фи2, Фи3)= R3*sin(Фи3)*sin(Фи2)*sin(Фи1)
    x2(Фи1, Фи2, Фи3)= R3*sin(Фи3)*sin(Фи2)*cos(Фи1)
    x3(Фи1, Фи2, Фи3)= R3*sin(Фи3}*cos(Фи2)
    x4(Фи1, Фи2, Фи3)= R3*cos(Фи3)

         а условия, накладываемые на углы для корректности (допустимости) аппроксимации при выполнении условий R1<<R3 и R2<<R3:

       sin(Фи3)>>R2/R3
       sin(Фи2)>>{R1/(R3*sin(Фи3)}

       Очевидно, что при приближении к оси x3 (третья координатная ось в евклидовой системе координат) cos(Фи2) стремится к 1, а sin(Фи3) стремится к 1 (при выполнении условий R1<<R3 и R2<<R3), поэтому ограничение на sin(Фи2), выглядит следующим образом:

       sin(Фи2)>>R1/R3

       При измерении используемых углов (полярных координат) в радианах, при приближении к координатным осям, когда соответствующие углы достаточно малы и выполняются условия sin(Фи3)<<1 или sin(Фи2)<<1, соответственно выполняются соотношения: sin(Фи3) примерно равно Фи3 или соответственно sin(Фи2) примерно равно Фи2. Поэтому условия корректности используемой аппроксимации выглядят следующим образом:

       Фи3>>R2/R3
       Фи2>>R1/R2

       Аналогично, строго говоря, рассматриваемый трехмерный гипертор, при выполнении условий R1<<R3 и R2<<R3, в указанной области углов аппроксимируется четырьмя вложенными друг в друга деформированными трехмерными гиперсферами переменных радиусов, и эти радиусы близки к R3 и различаются на аналогичные величины.

       А именно: в полярных координатах рассматриваемый трехмерный гипертор, при выполнении условий R1<<R3 и R2<<R3, в указанной области углов Фи1, Фи2, Фи3 аппроксимируется четырьмя вложенными друг в друга деформированными трехмерными гиперсферами переменных радиусов, и эти радиусы близки к R3 и различаются и различаются между такими соседними гиперсферами на следующие величины:

       при условии R2>R1 или R2=R1
       2R1*sin(уг.Фи3)*sin(уг.Фи2);
       2R2*sin(уг.Фи3)-2R1*sin(уг.Фи3)*sin(уг.Фи2);
       2R1*sin(уг.Фи3)*sin(уг.Фи2),

       и равны соответственно:
      
       R3+R2*sin(уг.Фи3)+R1*sin(уг.Фи3)*sin(уг.Фи2) - для первой (внешней) гиперсферы;
       R3+R2*sin(уг.Фи3)-R1*sin(уг.Фи3)*sin(уг.Фи2) - для второй гиперсферы;
       R3-R2*sin(уг.Фи3)+R1*sin(уг.Фи3)*sin(уг.Фи2) - для третьей гиперсферы;
       R3-R2*sin(уг.Фи3)-R1*sin(уг.Фи3)*sin(уг.Фи2) - для четвертой (внутренней) гиперсферы;

       при условии R1>R2
       2R2*sin(уг.Фи3)
       2R1*sin(уг.Фи3)*sin(уг.Фи2)-2R2*sin(уг.Фи3)
       2R2*sin(уг.Фи3)
 
       и равны соответственно начиная от внешней гиперсферы:
      
       R3+R2*sin(уг.Фи3)+R1*sin(уг.Фи3)*sin(уг.Фи2) - для первой (внешней) гиперсферы;
       R3-R2*sin(уг.Фи3)+R1*sin(уг.Фи3)*sin(уг.Фи2) - для второй гиперсферы;
       R3+R2*sin(уг.Фи3)-R1*sin(уг.Фи3)*sin(уг.Фи2) - для третьей гиперсферы;
       R3-R2*sin(уг.Фи3)-R1*sin(уг.Фи3)*sin(уг.Фи2) - для четвертой (внутренней) гиперсферы;   

       В дальнейшем эти формулы пригодятся нам для аппроксимации, в том числе, сферически деформированного трехмерного гипертора трехмерной гиперсферой.



       А теперь кратко рассмотрим условия аппроксимации трехмерного гипертора (трехмерного тора T3-R4) трехмерной гиперсферой (трехмерной сферой S3-R4) для отдельного подвида указанного трехмерного гипертора, а именно для однократно вырожденного трехмерного гипертора (T3-R4-0), у которого радиус первой образующей окружности равен нулю (R1=0), для случая, когда R2<<R3. У такого трехмерного гипертора нет первой образующей окружности, вместо такой окружности у него есть точка, лежащая в начале координат, которая и является центром для всех его вторых образующих окружностей. Первой образующей поверхностью у такого однократно вырожденного трехмерного гипертора является двумерная сфера, центр которой совпадает с началом координат, а радиус этой двумерной сферы равен R2, то есть радиусу его вторых образующих окружностей. Можно сказать, что эта двумерная сфера образована всеми, а значит бесконечным количеством указанных вторых образующих окружностей.
 
        Уравнения однократно вырожденного трехмерного гипертора (T3-R4-0) в соответствующих радиально-тороидальных координатах:

   x1(уг.фи1, уг.фи2, уг.фи3)={[R2+R3*cos(уг.фи3)]*cos(уг.фи2)}*cos(уг.фи1)
   x2(уг.фи1, уг.фи2, уг.фи3)={[R2+R3*cos(уг.фи3)]*cos(уг.фи2)}*sin(уг.фи1)
   x3(уг.фи1, уг.фи2, уг.фи3)=[R2+R3*cos(уг.фи3)]*sin(уг.фи2)
   x4(уг.фи1, уг.фи2, уг.фи3)=R3*sin(уг.фи3)

         Здесь:
       R1=0 - радиус первой образующей окружности равен нулю;
       R2 - радиус второй образующей окружности;
       R3 - радиус третьей образующей окружности;
       угол фи3 (сокращенное обозначение - уг.фи3 или у.фи3) - угол между следующими двумя лучами (половинками прямых): первый луч - это луч, проходящий через описываемую точку трехмерной поверхности гипертора и исходящий из центра третьей образующей окружности, соответствующей этой описываемой точке; второй луч - это луч, исходящий из начала координат (центра указанной второй образующей окружности) и проходящий через центр соответствующей третьей образующей окружности;
       угол фи2 (сокращенное обозначение - уг.фи2 или у.фи2) - угол между следующими двумя лучами (половинками прямых): первый луч - луч, исходящий из начала координат (центра указанной второй образующей окружности) и проходящий через центр указанной третьей образующей окружности; второй луч - луч, исходящий из начала координат и являющийся проекцией первого луча на координатную плоскость (x1,x2);
       угол фи1 (сокращенное обозначение - уг.фи1 или у.фи1) - угол между следующими двумя лучами (половинками прямых): первый луч - луч, исходящий из начала координат, и являющийся при описании угла фи2 вторым лучом (лежащим в координатной плоскости (x1,x2)); второй луч - положительная часть координатной оси x1.

       Аналогично тому, как я сделал это ранее для невырожденного случая, в формулах вырожденного трехмерного гипертора выделим часть, соответствующую описанию трехмерной гиперсферы. Если в правой части нижеследующих формул оставить только часть, заключенную в квадратные скобки, мы получим уравнения трехмерной гиперсферы с радиусом равным R3. Если же сделать наоборот, то есть в правой части нижеследующих формул исключить только часть, заключенную в квадратные скобки, мы получим уравнения двумерной сферы с радиусом равным R2; причем эта двумерная сфера с радиусом равным R2 является первой образующей двумерной поверхностью для описываемого вырожденного трехмерного гипертора (T3-R4-0) (с радиусами образующих окружностей соответственно:  R1=0 радиус первой образующей окружности равен нулю;  R2 - радиус второй образующей окружности; R3 - радиус третьей образующей окружности).
 
     x1(у.фи1,у.фи2,у.фи3)= [R3*cos(у.фи3)*cos(у.фи2)*cos(у.фи1)] +R2*cos(у.фи2)*cos(у.фи1)

     x2(у.фи1,у.фи2,у.фи3)= [R3*cos(у.фи3)*cos(у.фи2)*sin(у.фи1)] +R2*cos(у.фи2)*sin(у.фи1)

     x3(уг.фи1,уг.фи2,уг.фи3)= [R3*cos(уг.фи3)*sin(уг.фи2)] +R2*sin(уг.фи2)
 
     x4(уг.фи1,уг.фи2,уг.фи3)=[R3*sin(уг.фи3)]

       Очевидно, что когда выполняется условия R2<<R3, то вышеприведенные формулы вырожденного трехмерного гипертора (T3-R4-0),  в определенном диапазоне углов аппроксимируются формулами описывающими в четырехмерном евклидовом пространстве трехмерную гиперсферу через используемые радиально-тороидальные координаты.

        Очевидно, что эта аппроксимация является некорректной для некоторых углов  фи3. Из вышеприведенных формул следуют условия, накладываемые на углы для корректности (допустимости) аппроксимации, при выполнении условия R2<<R3:

       cos(уг.фи3)>>R2/R3

       При выполнении условия R2<R3, соответствующий вырожденный трехмерный гипертор (T3-R4-0) получается самопересекающимся и двухслойным.  При x4=0, x3=0 расстояния между его ближайшими друг к другу (соседними) двумя слоями пространства, в направлении радиус вектора с началом в начале координат, будут равны 2R2. А более точно, при выполнении условия R2<<R3, вплоть до точек самопересечения, для всех возможных x3 и x4, расстояния между этими его слоями будут равны 2R2*cos(уг.фи3) (с точность до слагаемых порядка R2, пренебрегая слагаемыми порядка R2*(R2/R3) и меньшими).

        Такой самопересекающийся вырожденный трехмерный гипертор (T3-R4-0) в качестве областей самопересечения имеет только две точки с координатами:
        x1=0, x2=0, x3=0, x4=R3-R2*R2/R3 (приблизительно, с точность до слагаемых порядка R2*R2/R3, пренебрегая слагаемыми порядка  R2*(R2/R3)*(R2/R3) и меньшими);
        x1=0, x2=0, x3=0, x4= -(R3-R2*R2/R3) (приблизительно, с точность до слагаемых порядка R2*R2/R3, пренебрегая слагаемыми порядка  R2*(R2/R3)*(R2/R3) и меньшими).

        Поэтому, рассматриваемый вырожденный трехмерный гипертор (T3-R4-0), при выполнении условия R2<<R3, в указанной области углов аппроксимируется двумя вложенными друг в друга деформированными трехмерными гиперсферами переменных радиусов, и эти радиусы близки к R3 и различаются между такими соседними гиперсферами на следующие величины:
       2R2*cos(уг.фи3) (с точность до слагаемых порядка R2, пренебрегая слагаемыми порядка R2*(R2/R3) и меньшими).   
       Радиусы этих деформированных трехмерных гиперсфер (гиперэлипсоидов) равны соответственно начиная от внешней гиперсферы:
       R3+R2*cos(уг.фи3);
       R3-R2*cos(уг.фи3).
      
        В соответствующих полярных координатах, где углы для радиус-вектора описываемой точки отсчитываются от направлений соответствующих координатных осей x2; x3; x4, и обозначаются соответственно Фи1; Фи2; Фи3, где (Фи3=(1/2)*пи-фи3) и (Фи2=(1/2)*пи-фи2), Фи1=фи1,   указанные формулы вырожденного трехмерного гипертора аппроксимируются формулами трехмерной гиперсферы радиуса R3, как я уже это делал ранее для невырожденного трехмерного гипертора (T3-R4). А условия, накладываемые на углы для корректности (допустимости) аппроксимации при выполнении условия R2<<R3:

       sin(Фи3)>>R2/R3.

       При измерении используемых углов (полярных координат) в радианах, при приближении к координатным осям, когда соответствующие углы достаточно малы и выполняются условия sin(Фи3)<<1 соответственно выполняются соотношения: sin(Фи3) примерно равно Фи3. Поэтому условия корректности используемой аппроксимации выглядят следующим образом:

       Фи3>>R2/R3.
      
        Из вышеизложенного следует, что в полярных координатах рассматриваемый вырожденный трехмерный гипертор (T3-R4-0), при выполнении условия R2<<R3, в указанной области углов аппроксимируется двумя вложенными друг в друга деформированными трехмерными гиперсферами переменных радиусов, и эти радиусы близки к R3 и различаются между такими соседними гиперсферами на следующие величины:
       2R2*sin(Фи3) (с точность до слагаемых порядка R2, пренебрегая слагаемыми порядка R2*(R2/R3) и меньшими).   
       Радиусы этих деформированных трехмерных гиперсфер (гиперэллипсоидов) равны соответственно начиная от внешней гиперсферы:
       R3+R2*sin(Фи3);
       R3-R2*sin(Фи3).

       В полярных координатах при выполнении условия R2<<R3, вплоть до точек самопересечения, для всех возможных x1, x2, x3 и x4, расстояния между соседними слоями вырожденного трехмерного гипертора (T3-R4-0) будут равны 2R2*sin(Фи3) (с точность до слагаемых порядка R2, пренебрегая слагаемыми порядка R2*(R2/R3) и меньшими).



       Часть тринадцатая.
       Первая космологическая теория поля. Первичная гипотеза. Вторичные гипотезы.
       А теперь немного фантазии:
       Предположим, что описанный в предыдущей части самопересекающийся трехмерный гипертор, удовлетворяющий условиям R1<<R3 и R2<<R3, это и есть пространство нашей Вселенной. Эта гипотеза является первичной гипотезой первой космологической теории поля. Отсюда можно сделать несколько вторичных гипотез.
       Итак, геометрия пространства Вселенной в виде вышеуказанного самопересекающегося трехмерного гипертора, удовлетворяющего условиям R1<<R3 и R2<<R3, сразу же дает нам несколько длин, пригодных к использованию в качестве базовых физических масштабов Вселенной, а соотношения этих длин дают нам соответствующие соотношения масштаба. Самым большим масштабом является радиус третьей образующей окружности R3, он же равен радиусу наших вышеуказанных четырех вложенных друг в друга трехмерных гиперсфер с точностью до R2+R1, то есть равен радиусу нашей Вселенной. Остаются еще несколько длин, пригодных к использованию в качестве базовых физических масштабов Вселенной, а именно:
       во-первых, радиус второй образующей окружности R2, производным от которого является базовый физический масштаб 2R2, равный расстоянию между соответствующими вышеуказанными трехмерными гиперсферами при условии x4=0, в общем случае расстояние между этими гиперсферами равны 2R2*sin(уг.Фи3), при условии Фи3>>R2/R3 (и конечно же R1<<R3 и R2<<R3);
       во-вторых, радиус первой образующей окружности R1, производным от которого является базовый физический масштаб 2R1, равный расстоянию между соответствующими вышеуказанными трехмерными гиперсферами при условии x4=0, x3=0, в общем случае расстояние между этими гиперсферами равны 2R1*sin(уг.Фи3)*sin(уг.Фи2), при условии Фи3>>R2/R3 и Фи2>>R1/R2 (и конечно же R1<<R3 и R2<<R3);
       в-третьих, производная величина - "щель2" - равная R2*R2/R3, "второй" прогиб трехмерного гипертора в областях самопересечения;
       в-четвертых, производная величина - "щель1" - равная R1*R1/R3, "первый" прогиб трехмерного гипертора в областях самопересечения.

       При этом, логично предположить, например, что при условии R1<<R2:
R1*R1/R3 равен или сопоставим с планковской длиной, а R1 равен или сопоставим с комптоновской длиной W-бозонов, или u или d кварков, а R2 равен или сопоставим с комптоновской длиной электронов; R3 равен радиусу Вселенной.
       Не исключено также, что кратность 3 электрического заряда кварков может объясняться наличием трех прослоек, между вышеуказанными четырьмя слоями вышеуказанного трехмерного гипертора, выбранного нами в качестве модели пространства Вселенной.
       Логично также предположить, что сами значения R1, R2, R3 и их соотношения могут определять, хотя бы частично, многие законы физики и универсальные физические константы.
       Исходя из универсального принципа самоподобия логично предположить, что, например, u и d кварки имеют пространственную структуру повторяющую по форме пространственную структуру Вселенной, то есть геометрически являются самопересекающимися трехмерными гиперторами, и т.д. и т.п.
       Также логично предположить, что взаимодействие между вышеуказанными четырьмя слоями нашего самопересекающегося трехмерного гипертора, удовлетворяющего условиям R1<<R3 и R2<<R3, то есть взаимодействие между четырьмя вышеуказанными гиперсферами, образующими Вселенную, определяет также и взаимодействия гравитационного характера, наблюдаемые и интерпретируемые нами, как воздействие темной материи и темной энергии. При этом, по-видимому, сами мы можем непосредственно наблюдать либо трехмерное пространство только одной из этих трехмерных гиперсфер, вероятнее всего - пространство внешней гиперсферы, либо наблюдаемое нами трехмерное пространство Вселенной есть своего рода суперпозиция и результат взаимодействия всех четырех вышеуказанных вложенных друг в друга слоев трехмерного гипертора, представляющих из себя в указанной области параметров (Фи3>>R2/R3,  Фи2>>R1/R2,  R1<<R3 и R2<<R3) четыре вышеуказанных вложенных друг в друга трехмерных гиперсферы.


       Часть четырнадцатая.
       Физические смыслы вращений вокруг образующих окружностей.

       Указанные первая, вторые и третьи образующие окружности, будут использованы нами и при построении и исследовании сферически деформированного трехмерного гипертора, с помощью которого мы моделируем пространство нашей Вселенной. При этом для пространства нашей Вселенной указанные образующие окружности обретают самостоятельный физический смысл, как локально взаимно ортогональные направления вращения самого пространства Вселенной, определяющие несколько возможных поляризаций такого вращения и соответствующих вращательных колебаний. При решении квантовой задачи для пространства Вселенной соответствующие этим окружностям направления вращения пространства Вселенной возможно приобретают следующие физические смыслы: для вращения и (или) вращательных колебаний пространства Вселенной вдоль третьей (или первой?) образующей окружности - смысл глобального внешнего момента импульса, как для самого пространства Вселенной, так и всех элементарных частиц; для вращения и (или) вращательных колебаний пространства Вселенной вдоль второй образующей окружности - смысл глобального первого внутреннего момента импульса и смысл электрического заряда, а точнее смысл физического свойства ответственного за электрическое и слабое взаимодействия, как для самого пространства Вселенной, так и всех элементарных частиц; для вращения и (или) вращательных колебаний пространства Вселенной вдоль первой (или третьей?) образующей окружности -  смысл глобального второго внутреннего момента импульса и смысл физического свойства, ответственного за сильное взаимодействие, как для самого пространства Вселенной, так и всех элементарных частиц.


       Часть пятнадцатая.
       Возможные апроксимации пространства сферически деформированного трехмерного гипертора.

       Пространство нашего само-соприкасающегося в центре его симметрии сферически деформированного трехмерного гипертора, рассматриваемого нами в четырехмерном евклидовом пространстве, для исследования его динамической геометрии в рамках классической (не квантовой) задачи (а в некоторых приближениях и для решения квантовой задачи) удобно аппроксимировать трехмерной поверхностью, которую удобно разбить на две части (сегмента). Первая часть (сегмент), соответствующая усеченному у полюсов нашему закрытому сферически деформированному трехмерный гипертору (первой части нашего закрытого сферически деформированного трехмерного гипертора), является усеченной у полюсов трехмерной гиперсферой. Указанные сечения и полюсы определяются постоянным значением (|x3|=const) координаты третьей координатной оси x3. А вторая часть - это трехмерная воронкообразная поверхность таким же образом усеченная у тех же полюсов этого трехмерного гипертора, расходящаяся от центра симметрии этого гипертора, находящегося в точке S, к  полюсам этого гипертора вдоль его оси симметрии, являющейся его третьей координатной осью, и заканчивающаяся у этих полюсов на границе с той частью поверхности этого трехмерного гипертора, которая аппроксимируется соответствующей трехмерной гиперсферой. Указанные сечения и полюсы определяются тем же постоянным значением (|x3|=const) (что и у соответствующей усеченной у полюсов трехмерной гиперсферы) координаты третьей координатной оси x3. Указанная воронкообразная поверхность аппроксимирует ту часть нашего закрытого сферически деформированного трехмерного гипертора, которую мы назваем "Глобальной червоточиной Вселенной". При этом, мы считаем, что характер сферической деформации нашего трехмерного гипертора таков, что, воронкообразной поверхностью, расходящейся от центра нашего сферически деформированного трехмерного гипертора вдоль четвертой координатной оси можно пренебречь по крайней мере в первом приближении (но не для решения ряда квантовых задач), в силу ее достаточно плотного обжатия всеми деформированными третьими образующими окружностями при соответствующей сферической деформации, так как практически все третьи образующие окружности будут при этом деформированы в почти полуокружности с хордами и будут плотно прижаты к четвертой координатной оси своими хордами, представляющими из себя за исключением их центральной части, примыкающей к центру симметрии S и ограниченной трехмерной гиперсферой радиуса R1, практически прямолинейные отрезки, то есть будет иметь место плотное протяженное само-соприкосновение вдоль четвертой координатной оси, в силу чего переток энергии из центральной части нашего трехмерного гипертора будет значительно заблокирован из-за "бутылочного" запирания центральной части нашего трехмерного гипертора большим градиентом кривизны пространства в направлении четвертой координатной оси. А именно, в направлении четвертой координатной оси  кривизна пространства резко, в почти точке "бутылочного горлышка", а именно на границе гиперсферы радиуса R1, меняется с чрезвычайно больших положительных величин на чрезвычайно большие отрицательные, а затем резко сбрасывается до нуля.
        В четырехмерном евклидовом пространстве построения нашего трехмерного гипертора границами между этими двумя частями являются две двумерные сферы. Эти границы (две двумерные сферы) можно определить, как пересечение  соответствующей указанной трехмерной гиперсферы и соответствующей указанной трехмерной воронкообразной поверхности. В определенных приближениях в качестве такой трехмерной воронкообразной поверхности можно попытаться аппроксимировать следующими  трехмерными поверхностями вращения: трехмерным конусом вращения; трехмерным параболоидом вращения; трехмерной розой вращения, а точнее двумя примыкающими к третьей координатной оси x3 сегментами трехмерной розы вращения, заканчивающимися радиус-вектором максимальной для выбранной розы длины. Из указанных трехмерных поверхностей более всего соответствует реальной поверхности нашего сферически деформированного трехмерного гипертора именно трехмерная роза вращения.
       Указанные границы (две двумерные сферы) обладают  следующими свойствами: При построении нашего трехмерного гипертора  а в качестве начала координат  выбирали его центр симметрии, являющийся центром его первой образующей окружности (на рисунке ему соответствует точка S).  Тогда все точки указанных двумерных сфер, являющихся границами между указанными двумя частями  фигуры аппроксимирующей наш трехмерный гипертора, (и разумеется поэтому принадлежащие пространству этой фигуры) являются точками, имеющими одинаковое по модулю значение (x3=|const|) координаты третьей координатной оси x3 (являющейся одной из осей симметрии нашего трехмерного гипертора). Трехмерные евклидовы пространства  этих двумерных сфер параллельны трехмерному евклидову пространству, образованному плоскостью главной образующей окружностью нашего трехмерного гипертора и четвертой координатной осью. Это объясняется тем, что эти трехмерные пространства согласно условию x3=|const| сами образованы соответствующей плоскостью параллельной плоскости главной образующей окружности нашего трехмерного гипертора и четвертой координатной осью. Указанную воронкообразную трехмерную поверхность для упрощения задачи удобно аппроксимировать достаточно простой поверхностью вращения, например примыкающими к третьей координатной оси: трехмерным конусом вращения (x3)*(x3)= A((x1)*(x1)+(x2)*(x2)+(x4)*(x4));  трехмерным параболоидом вращения (x3)= B((x1)*(x1)+(x2)*(x2)+(x4)*(x4)); двумя примыкающими к третьей координатной оси x3 сегментами трехмерной розы вращения, заканчивающимися радиус-вектором максимальной для выбранной розы длины, совпадающей с длиной радиуса соответствующей трехмерной гиперсферы, выбранной в качестве аппроксимации указанной первой части поверхности нашего трехмерного гипертора.  Для трехмерного конуса вращения  и для трехмерного параболоида вращения, но не для трехмерной розы вращения, такие границы имеют максимальное (из всех точек нашего трехмерного гипертора)) по модулю значение (x3=|const|) координаты третьей координатной оси x3. Для трехмерной розы вращения в качестве такой границы удобнее выбирать максимальное значение амплитуды такой розы равное радиусу соответствующей трехмерной гиперсферы, что равно третьему главному образующему радиусу R3 нашего трехмерного гипертора. Далее я подробнее обосную, что наиболее интересной и близкой к реальности является указанная воронкообразная поверхность в виде трехмерной розы вращения.


       Часть шестнадцатая.
       Принцип эквивалентности пространства-времени и гравитации.
      
       Для предлагаемой динамической геометрии пространства и времени еще одним базовым постулатом - базовым принципом - моей концепции "глобального пространства" и "глобального времени" Вселенной является "Принцип эквивалентности пространства-времени и гравитации", к формулировке которого, как я считаю, вплотную подошел и сам Д.Е. Бурланков, особенно когда указывал, что принцип эквивалентности, известный из "Общей теории относительности" в рамках "Теории глобального времени" превращается из локального в глобальный. Согласно "Принципу эквивалентности пространства-времени и гравитации": гравитация не просто как по Эйнштейну обеспечивает кривизну пространства, гравитация не просто как по Бурланкову генерирует само пространство, обладающее уже как самостоятельный объект собственной энергией, в рамках моей концепции пространство-время и гравитация суть одно и то же, что является исходной гипотезой и исходным постулатом Принципа эквивалентности пространства-времени и гравитации. Согласно данному принципу пространство-время есть ни что иное как глобальное гравитационное поле, генерируемое в едином "глобальном времени" всей совокупностью гравитирующих объектов Вселенной, включая и само "глобальное пространство" как гравитирующий объект, а точнее все-таки глобальное пространство-время, о чем поговорим позднее.

      Полагаю, что само так называемое базовое бесконечное Евклидово пространство Вселенной, получаемое, как в рамках "Общей теории относительности", так и в рамках "Теории глобального времени", как пространство с нулевой энергией, есть ни что иное, как математическая абстракция, не соответствующая реальности. Это очевидно уже в рамках квантовой гипотезы самой "Теории глобального времени", поскольку квантовый подход изначально исключает реальность абсолютно нулевой энергии.


       Часть семнадцатая.
       Динамика изначальной геометрии Вселенной.

       Предлагаемая геометрия пространства Вселенной, как я полагаю, может предполагать два варианта изначальной геометрии. При этом наиболее вероятно, что они оба реализуются как последовательные стадии развития Вселенной. Наиболее вероятно, что первый вариант предшествует второму, а сам переход от первого варианта ко второму происходит не непрерывно, а скачком, имеющим квантовый характер, и неизбежно появляется как решение динамической квантовой задачи уже для гамильтониана соответствующего первому варианту. Первый вариант означает изначальное равенство всех трех (главных) образующих радиусов трехмерного гипертора (R1=R2=R3). Здесь (главные) образующие радиусы нашего трехмерного гипертора - это радиусы трех его (главных) образующих окружностей в четырехмерном пространстве его построения.
     На этой стадии анизотропия и неоднородность Вселенной проявляет себя уже в форме анизотропии и неоднородности пространства-времени, хотя пространственно-временные соотношения масштаба проявляются еще достаточно слабо, что выражается в самом равенстве R1=R2=R3. Этот вариант означает, что изначальная первая образующая (главная) двумерная поверхность трехмерного гипертора уже сформирована и представляет из себя двумерный само-соприкасающийся тор, который замкнут в точку, являющуюся его центром симметрии. А сам изначальный трехмерный гипертор является самопересекающимся, то есть имеет трехмерную поверхность дополнительной связности, находящуюся внутри его трехмерной поверхности главной (основной) связности и расположенную в среднем ближе к его центру симметрии. Однако, данное кантовое состояние является состоянием неустойчивого равновесия и первый вариант путем квантового скачка или, что более вероятно, серии квантовых скачков преобразуется во второй вариант с видоизмененной геометрией пространства и соответственно с другим распределением энергии, хотя полная энергия сохраняется, так как закон сохранения энергии действует.

     Второй вариант соответствует другому возможному соотношению этих радиусов, а именно R1=2*R2=2*R3. Второй вариант означает, что сам изначальный трехмерный гипертор является само-соприкасающимся, то есть замкнутым в точку, являющуюся его центром симметрии, и не имеет поверхностей дополнительной связности.  А его первая образующая двумерная поверхность является при этом открытым двумерным тором (имеющим форму булика с дыркой посередине).      
     При этом выполнение условия R1=2*R2=2*R3 вероятнее всего уже означает отделение гравитации от других типов взаимодействия, поскольку возникает соответствующее соотношение масштабов и появляются предпосылки для возникновения центростремительной силы. С момента выполнения этого условия развитие геометрии нашего трехмерного гипертора (пространства Вселенной) вступает в стадию розы (об этом ниже).
      Сам переход от первого варианта ко второму предполагает такое разрушение трехмерной поверхности дополнительной связности, которое происходит в виде огромнейшего числа ее разрывов, что должно сопровождаться колоссальным выбросом энергии и самозамыканием мельчайших обрывков этой трехмерной поверхности дополнительной связности в мельчайшие трехмерные гиперсферы, а возможно и (или) в мельчайшие трехмерные гиперторы (не путать с нашим трехмерным гипертором - трехмерным пространством нашей Вселенной) или, что менее вероятно, еще и в иные простейшие трехмерные поверхности без границы, которые могут касаться (в отдельных своих точках) друг друга, а также могут касаться (в отдельных своих точках, в том числе и протяженными участками одномерных линий или двумерных поверхностей) поверхности нашего трехмерного гипертора, и расположенные внутри (не исключено, что и снаружи) трехмерной поверхности нашего трехмерного гипертора (но не на этой трехмерной поверхности, а в четырехмерной области гиперполнотория, ограниченной этой трехмерной поверхностью (не исключено, что и снаружи этой области)), и образующие первичную подпространственную пену, являющуюся первичной темной материей. В результате такого касания эта темная материя деформирует трехмерное пространство нашей Вселенной, что проявляется в виде гравитации. Но поскольку эта темная материя не принадлежит трехмерному пространству нашей Вселенной, и, в отличие от трехмерного пространства нашей Вселенной и существующих в ней элементарных частиц  не является решением или собственными функциями соответствующей квантовой задачи, эта темная материя никаким другим образом не взаимодействует с имеющейся в нашей Вселенной материей (веществом и полями). Этот переход от первого варианта ко второму происходит также с образованием в самом трехмерном пространстве Вселенной (на трехмерной поверхности нашего трехмерного гипертора) кварк-глюонной плазмы, либо предшествовавшей ей более разнообразной плазмы, например первичной плазмы суперструн. Этот момент соответствует моменту образования такой плазмы в теории Большого взрыва.


       Часть восемнадцатая.
       Элементарные частицы стандартной модели, как решения и собственные функции глобального квантового уравнения для пространства Вселенной.

       Здесь стоило бы рассмотреть более простые построения, чем теория суперструн, например, простейшие трехмерные поверхности без границы и с границей и их простейшие колебания, например трехмерные: гиперсфера (род 0) в качестве бозона Хиггса; трехмерный тор (гипертор) T3-R4 (род 1) в качестве u и d кварков и антикварков; гипервосьмерка (род 2) в качестве  c и s кварков и антикварков; гипербрецель (род 3) в качестве  t и b кварков и антикварков; вещественная проективная гиперплоскость (род 1) в качестве электрона и позитрона (ее самопересекающееся вложение в четырехмерное евклидово пространство: диск с пленкой Мебиуса; ее локальные не самопересекающиеся погружения в четырехмерное евклидово пространство: гиперповерхность Боя; Римская гиперповерхность); гипер Бутылка Клейна (род 2) в качестве мюона и анти-мюона; гиперповерхность Дика (род 3) в качестве тау и анти-тау; гиперконус в качестве фотона; гипер самопересекающийся диск в качестве нейтрино и антинейтрино; гипер дважды самопересекающийся диск в качестве мюонного нейтрино и мюонного антинейтрино; гипер трижды самопересекающийся диск в качестве тау нейтрино и тау антинейтрино, и т.д. и т.п. ...  В основе данной идеи лежит универсальный принцип самоподобия. Однако для еще большего соответствия не только принципу самоподобия, но и принципу нелокальной связанности Вселенной, стоило бы рассмотреть все поля элементарных частиц в качестве нелокально взаимодействующих трехмерных много-угловых роз, в частности переменных трехмерных трех-угловых роз (простейшие формулы которых приведены ниже), которые модулируют вышеуказанные простейшие трехмерные поверхности без границы (гиперсферу; гипертор; гипервосьмерку; гипербрецель; вещественную проективную гиперплоскость; гипер Бутылку Клейна; гиперповерхность Дика, и т.д.) в трехмерные поверхности топологически эквивалентные им, но имеющие главный центр в соответствующем четырехмерном пространстве, совпадающий с центром симметрии нашей Вселенной (нашего трехмерного гипертора), и имеющие переменный ограничивающий радиус, не меньше, чем третий главный образующий радиус R3 нашего трехмерного гипертора (нашей Вселенной). Точнее положения их центров и соответствующих групп их центров, для области окружающей центр симметрии нашей Вселенной (нашего трехмерного гипертора), необходимо рассматривать с учетом расслоения Хопфа или соответствующего вещественного расслоения (не исключены, но маловероятны, и варианты с кватернионной или октавной версиями расслоений), а при учете вращения Вселенной вокруг ее оси симметрии (третьей координатной оси нашего трехмерного гипертора) - с учетом кватернионного расслоения, а при учете более сложных вращений Вселенной вдоль вторых и третьих образующих окружностей - с учетом октавного расслоения. Тогда наблюдаемые поля (части полных полей) элементарных частиц и черных дыр можно рассматривать, как пересечения отдельных лепестков этих топологически преобразованных трехмерных роз с нашим трехмерным гипертором (нашей Вселенной). При этом сами эти поля (полные трехмерные поверхности, а не только соответствующие пересечения) неизбежно топологически пересекаются в области центра Вселенной, что и обеспечивает их нелокальное взаимодействие. Причем эти поля и соответствующие им топологически преобразованные трехмерные розы должны появляться, как решения или собственные функции уравнений Шредингера (волновые функции) для энергетических распределений, соответствующих вышеуказанным решениям для нашего трехмерного гипертора (нашей Вселенной). Таким образом и указанные поля элементарных частиц (модулированные указанными розами указанные трехмерные поверхности и само пространство Вселенной также является продуктом и решением одной и той же соответствующей динамической квантовой задачи для соответствующего гамильтониана, то есть начального распределения гравитационной энергии в некоторой начальной геометрии пространства. То есть наш поначалу эвристический принцип эквивалентности пространства и гравитации обретает при этом новый смысл, как решение соответствующей квантовой задачи. Таким образом, мы в первом приближении как раз и приходим к Единой теории поля, включающей все виды взаимодействия, а сама квантовая теория поля в некотором смысле превращается при этом из науки микромира в науку космологическую. Тоже самое в принципе можно проделать и с объектами теории суперструн (M-теории), модулируя суперструны розами, или хотя бы сделать сами суперструны космическими объектами с линейной длиной превышающей радиус Вселенной. Но на мой взгляд использование суперструн только приведет к ненужному усложнению теории, поскольку для формулировки и математически строгого решения соответствующей квантовой задачи нам придется вводить несколько дополнительных, пусть и свернутых, пространственных измерений в геометрию нашего пространства Вселенной. Виртуальные частицы и виртуальные частицы вакуума в рамках такой концепции следует рассматривать, как розы с бесконечно большим K(t) (конечно же с условно бесконечно большим, то есть с достаточно большим, на много порядков больше, чем для роз прочих частиц), поэтому такие розы (поля в виде трехмерных поверхностей) виртуальных частиц я предлагаю называть "струнами времени". Именно пространственно-временная деформация "струн времени" (полей виртуальных частиц) в процессе взаимодействия частиц, в том числе их столкновений высоких энергий, приводит к образовыванию новых не виртуальных частиц. Гравитационное поле любой черной дыры в рамках такой теории - это модулированный лепестком такой гигантской розы трехмерный гипертор. Соответствующую космологическую квантовую теорию поля я называю: "Теория великих роз" или "GR-теория". Однако, для подробного представления основ этой теории понадобится отдельная статья.


       Часть девятнадцатая.
       Дальнейшее развитие геометрии пространства Вселенной.


       В дальнейшем развитие геометрии нашего трехмерного гипертора предполагает его деформацию, обеспечивающую отсутствие или минимальное присутствие поверхностей дополнительной связности. На этой стадии анизотропия и неоднородность Вселенной и  пространственно-временные соотношения масштаба проявляются уже достаточно сильно.
     Опираясь на предлагаемый принцип эквивалентности пространства и гравитации логично предположить, что после реализации указанного второго варианта с отделением гравитации от других типов взаимодействия, то есть с возникновением гравитации, как самостоятельного поля, имеющего относительно его точечных источников исключительно центростремительное сферическое действие, происходит сферическая деформация полученного трехмерного гипертора, при которой подавляющая часть его поверхности (кроме поверхности вблизи его оси симметрии) будет асимптотически стремиться к поверхности соответствующей гиперсферы с радиусом равным R3. Такая деформация предполагает выполнение следующего соотношения: R1<<R2<<R3.

       Для нас главной особенностью такой сферической деформации является появление на ее первой стадии и обязательное последующее сохранение единой точки пересечения всех вторых образующих деформированных окружностей. Это означает, что первая двумерная образующая окружность нашего трехмерного гипертора, имеющая форму тора, вновь становится само-соприкасающейся и замкнутой в единственной точке S.  Причем переход к этому состоянию также происходит не непрерывно, а скачком или серией скачков, имеющих квантовый характер. То есть сначала мы снова приходим к выполнению условия R1=R2, но третьи образующие окружности при этом уже не образуют поверхностей дополнительной связности, и наш трехмерный гипертор остается само-соприкасающимся в своем центре симметрии. При этом так же остается само-соприкасающейся и вторая двумерная  образующая поверхность, преобразованная в этом случае в соответствующий деформированный двумерный тор. То есть здесь и далее сферическая деформация происходит с сохранением в целом формы и связностей трехмерного гипертора. При этом R3 будет величиной непостоянной в пространстве, меняющейся практически от 0 (у цента симметрии нашего трехмерного гипертора), до R2 (на его экваторе x3=0, когда центр третьей образующей окружности максимально удален от цента симметрии нашего трехмерного гипертора). Результат такого перехода к R1=R2 предполагает полное отсутствие или последующее минимальное присутствие поверхностей дополнительной связности нашего трехмерного гипертора. При этом вероятнее всего сильное взаимодействие уже отделяется от электрослабого, после чего начинается уменьшение R2 по сравнению с R3 (или увеличение R3 по сравнению с R2) и начинается вторая стадия вышеуказанной сферической деформации нашего трехмерного гипертора с выполнением и усилением условия R1<<R2<<R3 и отделением при некотором соотношении R2 и R3 электромагнитного взаимодействия от слабого. На рисунке мы видим пересечение всех вторых образующих окружностей в точке S до их сферической деформации. Для нас важно выполнение хотя бы одного из следующих условий, а именно: либо необходимо, чтобы все деформированные третьи (главные) образующие окружности также пересекались в точке S, для чего необходимо, чтобы R1 был равен нулю; либо, чтобы каждая соответствующая деформированная третья образующая окружность пересекала диск (деформированный круг) деформированной второй образующей окружности, на которой находится центр этой третьей образующей окружности, в смещенном деформацией центре этой второй образующей окружности (находящимся на расстоянии R1 от центра симметрии нашего трехмерного гипертора), что означает, что вторая образующая поверхность нашего трехмерного гипертора остается само-соприкасающейся. При этом в области соответствующего четырехмерного пространства построения и трехмерного пространства Вселенной, которая ограничивается соответствующими сферами величины R2 (не путать с трехмерным пространством построения ограниченным соответствующей заданной R2 образующей поверхностью), должна содержаться почти вся энергия, изначально генерирующая образование всего пространства Вселенной. Не исключено, что эта область может быть многосвязной, то есть некоторые третьи образующие окружности пересекаются между собой в двух точках. При этом необходимо, чтобы каждая соответствующая деформированная третья образующая окружность пересекала диск (деформированный круг) деформированной второй образующей окружности, на которой находится центр этой третьей образующей окружности на отрезке между центром этой второй образующей окружности (находящимся на расстоянии R1 от центра симметрии нашего трехмерного гипертора) и центром симметрии нашего трехмерного гипертора. Вводя эти условия пересечения, мы также боремся за сохранение простоты конструкции и описания нашего глобального пространства Вселенной и сохранение плоской евклидовой формы вторых и третьи образующих окружностей, что делается нами исходя из принципа энергетической эффективности Вселенной, который приводит в итоге к максимальной математической простоте физических законов. После подобного пересечения или почти пересечения этих третьих образующих деформированных окружностей в точке S происходит появление пространства-времени в привычном нам современном виде.
      
       При этом проявляется одно из очевидных преимуществ тороидальной геометрии Вселенной над сферической геометрией. Это преимущество состоит в том, что геометрический центр симметрии Вселенной при такой тороидальной геометрии принадлежит самой трехмерной поверхности нашего трехмерного гипертора, то есть принадлежит трехмерному пространству Вселенной, а при сферической геометрии центр симметрии Вселенной не может быть обнаружен в трехмерном пространстве Вселенной. Поэтому только при подобной тороидальной геометрии мы можем обнаружить непосредственно в трехмерном пространстве Вселенной, а именно в центре симметрии Вселенной, некий глобальный гравитирующий физический объект, являющийся изначальным источником всей энергии Вселенной, и генерирующий всю наблюдаемую энергию Вселенной, том числе и наблюдаемое расширение Вселенной, интерпретируемое, в том числе, как темная энергия.  Такой физический объект я предлагаю назвать "Черная дыра Вселенной". Хотя этот объект, накачивая пространство-время энергией, в настоящее время ведет себя не как традиционная черная дыра, а скорее как гипотетический объект называемый белой дырой, я все же предлагаю назвать его "Черной дырой Вселенной", поскольку такое название более широко известно и хорошо отражает тот факт, что этот объект содержит огромное количество энергии (материи) вероятно многократно превышающее энергию всего остального пространства-времени. В рамках предлагаемого "Принципа эквивалентности пространства-времени и гравитации" логично предположить, что изначально все, а впоследствии в основном все вышеописанное пространство-время Вселенной, в том числе и "глобальное время" также генерируется этим глобальным сверх-массивным вращающимся с прецессией гравитирующим объектом, который я называю "Черной дырой Вселенной". Разумеется, что при этом и вся порожденная Черной дырой Вселенной видимая материя, темная материя и само глобальное пространство-время  взаимодействуют с Черной дырой Вселенной и, таким образом, влияют на характеристики глобального пространства-времени.

       В привычном нам квазиевклидовом трехмерном пространстве мы можем представить себе аналог такого само-соприкасающегося замкнутого в точку (или самопересекающегося в области центра симметрии) сферически деформированного трехмерного гипертора, (являющегося ограничивающей поверхностью соответствующего объемного замкнутого в точку сферически деформированного четырехмерного гиперполнотория), как поверхность апельсина с удаленными кожицей и осевой сверхтонкой несъедобной жилкой, или как поверхность состоящую из стелющихся вдоль поверхности Земли и уходящих в полюса линий ее магнитного поля. Но, еще полезнее представить себе такой аналог в виде наружной поверхности накачанной воздухом тороидальной резиновой камеры без отверстия в ее середине (вдоль оси тора). При таком представлении этого аналога легко себе представить и сферическую деформацию соответствующего тора, для этого такую тороидальную резиновую камеру необходимо втиснуть в сферу чуть большего объема, чем объем этой тороидальная камера. Поскольку почти вся поверхность деформированной таким образом резиновой тороидальной камеры будет повторять или почти повторять поверхность сферы, в которую мы ее втиснули, становится понятным, что радиус R1 первой образующей окружности (первый образующий радиус R1) будет уменьшаться, стремясь к нулю. Вторая образующая окружность при такой деформации преобразуется в фигуру близкую (близко вписанную) к полуокружности со стягивающей ее концы хордой, то есть полученная фигура напоминает плоскую грань апельсиновой дольки. Такая деформированная вторая образующая окружность уже будет иметь радиус R2 равный радиусу сферы, в которую мы втиснули нашу тороидальную резиновую камеру. А ее сильно деформированная часть, близкая к хорде длиной 2*R2, будет похожа на дугу окружности с радиусом много больше, чем R2. Причем все такие деформированные вторые образующие окружности пересекаются только на серединах таких дуг в точке S.

       Для нас важно так же, что главная образующая двумерная поверхность нашего трехмерного гипертора, определяемая главными радиусами R1 и R2, как раз и будет иметь форму поверхности такого очищенного апельсина или наружной поверхности такой сферически деформированной резиновой тороидальной камеры.

       Каждая из точек первой образующей двумерной поверхности нашего трехмерного гипертора является центром соответствующей его третей главной образующей окружности, имеющей радиус R3. Эта третья главная образующая окружность лежит в плоскости ортогональной (перпендикулярной) трехмерному пространству, в котором находится указанная главная образующая двумерная поверхность. Плоскость этой третьей главной образующей окружности пересекается с плоскостью соответствующей второй главной образующей окружности, на которой находится центр этой третьей главной образующая окружность, по прямой, проходящей через центры этих окружностей (центр этой третьей главной образующая окружности и центр указанной соответствующей второй главной образующей окружности). На нашем рисунке в качестве такого центра третьей главной образующей окружности может, для примера, быть выбрана точка P. Соответствующей второй главной образующей окружностью,(на которой находится центр этой третьей главной образующей окружности), в этом случае является окружность, проходящая через точки P и S. А прямой, являющейся пересечением плоскости соответствующей третьей главной образующей окружности и плоскости этой второй главной образующей окружности, является прямая, проходящая, через точки M и P. Однако, для построения такой плоскости третьей главной образующей окружности необходимо уже использовать четвертое измерение, ортогональное всему трехмерному пространству, в котором мы построили главную образующую двумерную поверхность нашего трехмерного гипертора. Поэтому соответствующая четвертая ось должна быть ортогональна не только плоскости второй главной образующей окружности, но и плоскости первой главной образующей окружности. Соответственно на нашем рисунке мы не можем изобразить саму третью главную образующую окружность, поскольку ее плоскость ортогональна (перпендикулярна) изображенному трехмерному пространству, и пересекается с ним только по указанной прямой.
     Геометрический образ третей главной образующей окружности и образ соответствующего трехмерного гипертора в четырехмерном пространстве нам крайне сложно представить, поскольку мы оперируем привычными нам трехмерными образами. Для нас пока важно то, что при соответствующей сферической деформации нашего трехмерного гипертора его третья главная образующая окружность деформируется аналогично его второй главной образующей окружности, а именно преобразуется в фигуру близкую (близко вписанную) к полуокружности со стягивающей ее концы хордой (напоминает плоскую грань апельсиновой дольки).

     Поэтому область трехмерного пространства Вселенной, образованная соответствующими близкими к хордам дугами, стягивающими указанные полуокружности третьих главных образующих окружностей, будет являться "Глобальной червоточиной Вселенной", проходящей через "Черную дыру Вселенной". Безусловно, наличие такой "Глобальной червоточины Вселенной" является главным парадоксом предлагаемой теории, поскольку при движении по этой червоточине к "Черной дыре Вселенной" оборачивается вспять само локальное время в привычном нам понимании. Однако и без сферической деформации тороидальной геометрии пространства-времени нам обойтись крайне сложно, поскольку без выполнения условия R1<<R2<<R3 может исчезать однозначность и возникать многозначность глобального времени, в этом случае обособленного для каждой в отдельности третьей главной образующей окружности.
     Кроме того, именно то обстоятельство, что средняя кривизна трехмерной поверхности нашего трехмерного гипертора (без учета трехмерной поверхности являющейся "Глобальной червоточиной Вселенной") больше средней кривизны самой "Глобальной червоточиной Вселенной" (которая может быть и отрицательной в случае когда стягивающие хорды являются вогнутыми дугами), как раз и обеспечивает переток энергии от "Черной дыры Вселенной" к остальной области трехмерного пространства Вселенной.  Для расчетов и сшивки решений на границе "Глобальной червоточины Вселенной" с остальной Вселенной, имеющей форму близкую к трехмерной гиперсфере, нам необходимо определить или выбрать удобную и реалистичную форму геометрии "Глобальной червоточины Вселенной". Примерами таких форм могут быть следующие трехмерные поверхности: трехмерный конус; трехмерный гиперболоид; трехмерный параболоид; два сегмента трехмерной одноугловая розы, примыкающие к оси симметрии Вселенной, пробегающие значения модуля радиус-вектора от 0 до R3; два сегмента трехмерной многоугловой розы, примыкающие к оси симметрии Вселенной, пробегающие значения модуля радиус-вектора от 0 до R3. Вторая и третья из перечисленных поверхности имеют отрицательную кривизну относительно центра симметрии Вселенной, а четвертая и пятая - положительную. Если считать, что "Глобальная червоточина Вселенной" имеет форму близкую к трехмерной поверхности трехмерного гиперболоида, необходимо учесть, что такой гиперболоид не может быть закрытым в центре симметрии нашего трехмерного гипертора, поэтому для обеспечения закрытости такая форма нуждается в дополнении еще одной трехмерной поверхностью в области этого центра симметрии, которая пересекается с трехмерной поверхностью такого гиперболоид что делает результирующую суммарную поверхность многосвязной (многослойной).
     А указанная остальная область пространства-времени Вселенной имеет форму близкую к усеченной у полюсов трехмерной гиперсфере (как я уже указывал ранее) и обладает поэтому положительной кривизной, и в силу этого имеет способность накапливать энергию не увеличивая плотность этой энергии, а увеличивая свой радиус R3, то есть наименее энергоемким способом. Такой способ получения и накапливания энергии этой почти гиперсферической областью пространства-времени, в случае исчерпания потока энергии от накачивающей эту область "Черной дыры Вселенной", вероятнее всего обеспечивает последующее сжатие этой области в саму "Черную дыру Вселенной". Здесь выражение "вероятнее всего" следует понимать в том смысле, что вероятнее всего наша Вселенная замкнутый объект и не имеет подкачки энергии от других вселенных. В этом случае любая самая глобальная динамика в самом глобальном виде представляет  из себя циклоиду, в общем случае циклоиду с переменными параметрами. При этом я исхожу из предположения, что наблюдаемое расширение Вселенной это и есть часть самой глобальной динамики, а значит часть цикла расширение-сжатие Вселенной. При таком сжатии связь с самой областью "Черной дыры Вселенной" может полностью рваться, например вследствие полного исчерпания энергии "Черной дыры Вселенной". При таком сжатии "Глобальная червоточина Вселенной" может полностью исчезать (например теряя свою отрицательную кривизну), а сама соответствующая область пространства-времени Вселенной, близкая к трехмерной гиперсфере, в этом случае полностью преобразуется в сжимающуюся (уменьшающую свой радиус) трехмерную гиперсферу.
    Такую динамику несложно проверить математически. При этом задача (при соответствующей апроксимации) сводится к двум довольно простым задачам для двух вышеуказанных трехмерных поверхностей (двух частей нашего трехмерного гипертора: трехмерной усеченной гиперсферы и трехмерной поверхности "Глобальной червоточины Вселенной"), из которых и состоит наш замкнутый сферически деформированный трехмерный гипертор - наша Вселенная (трехмерная поверхность нашего объемного четырехмерного гиперполнотория)  с последующей сшивкой решений. А именно: Первая задача - это задача трехмерной поверхности "Глобальной червоточины Вселенной" с точечным источником энергии в ее центре (в центре симметрии нашего гипертора) и с двумя стоками энергии в виде двумерных сфер (в искусственно упрощенной задаче в виде обычных одномерных окружностей), расположенных в области полюсов нашего трехмерного гипертора (трехмерной поверхности четырехмерного гиперполнотория в четырехмерном пространстве-времени Вселенной). Именно такая двумерная сфера как раз и будет являться сечением трехмерной поверхности "Глобальной червоточины Вселенной" и соответственно трехмерной поверхности нашего трехмерного гипертора евклидовым трехмерным пространством, параллельным трехмерному евклидовому экватору нашего гипертора (в нашем четырехмерном пространстве построения) и пересекающем (касающимся для трехмерных поверхностей "Глобальной червоточины Вселенной" в виде конуса вращения или параболоида вращения) эту трехмерную поверхность (являющейся нашей Вселенной) нашего трехмерного гипертора  у его полюса, при такой по модулю координате третьей координатной оси x3 и радиусе этого сечения, при которых начинается область, совпадающая с усеченной у полюсов трехмерной гиперсферой. (Указанный экватор это трехмерная евклидова поверхность ортогональная оси симметрии нашего трехмерного гипертора, включающая плоскость экватора его двумерной образующей поверхности и прямую ортогональную трехмерному евклидову пространству, в котором строится эта двумерная образующая поверхность. Такой экватор рассекает наш трехмерный гипертор на две симметричные относительно этого экватора части.) Вторая задача - это задача для трехмерной поверхности усеченной у полюсов гиперсферы с двумя источниками энергии в виде двумерных сфер (в искусственно упрощенной задаче в виде обычных одномерных окружностей), расположенных в области этих усечений. Эти источники как раз и будут в такой схеме являться вышеуказанными стоками энергии для вышеуказанной воронкообразной трехмерной поверхности  "Глобальной червоточины Вселенной".
    (Как я уже описывал выше: "В четырехмерном евклидовом пространстве построения нашего трехмерного гипертора границами между этими двумя частями нашего трехмерного гипертора являются две двумерные сферы (две двумерные окружности). Эти границы (двумерные сферы (двумерные окружности)) можно определить следующим образом: При построении нашего трехмерного гипертора в качестве третьей координатной оси мы выбирали его ось симметрии, а в качестве начала координат  выбирали его центр симметрии, лежащий на этой оси (на рисунке это точка S). Этот центр симметрии является (само собой разумеется) центром первой главной образующей окружности нашего трехмерного гипертора. Тогда все точки указанных двумерных сфер (двумерных окружностей), являющихся границами между указанными двумя частями  нашего трехмерного гипертора, (и разумеется поэтому принадлежащие пространству нашего трехмерного гипертора,) являются точками, имеющими одинаковое по модулю значение координаты третьей координатной оси x3 (совпадающей с осью симметрии нашего трехмерного гипертора). Трехмерные пространства (трехмерные плоскости) этих двумерных сфер (двумерных окружностей) параллельны трехмерному пространству (трехмерной плоскости), образованному плоскостью главной образующей окружностью нашего трехмерного гипертора и четвертой координатной осью. Это объясняется тем, что эти трехмерные пространства согласно условию x3=|const| сами образованы соответствующей плоскостью параллельной плоскости главной образующей окружностью нашего трехмерного гипертора и четвертой координатной осью".)
    Таким образом, обе задачи - это задачи для двух ограниченных областей пространства (двух частей нашего трехмерного гипертора) с соответствующими источниками или стоками энергии на границах этих областей. При этом каждая из этих областей пространства имеет простую конфигурацию для одного и того же момента глобального времени. Поэтому соответствующие решения довольно легко получаются и имет весьма простой вид.  Для обеих областей решение после сшивки - это расширяющийся трехмерный гипертор указанной формы и конфигурации с увеличивающимся радиусом R3 и соответственно с пространством, кривизна которого для обеих областей (двух частей нашего трехмерного гипертора) стремится к нулю. При исчерпании источника энергии получаем последующее сжатие нашего гипертора (нашей Вселенной) или неограниченное расширение (при преобладании кинетической энергии расширения пространства). Результат с неограниченным последующем расширением маловероятен в силу причин схематически описанных выше.
     Однако, наибольший интерес для нас имеют две последние из рассматриваемых форм трехмерной поверхности "Глобальной червоточины Вселенной", а именно:  два сегмента трехмерной одноугловая розы, примыкающие к оси симметрии Вселенной, пробегающие значения модуля радиус-вектора от 0 до R3; два сегмента трехмерной многоугловой розы, примыкающие к оси симметрии Вселенной, пробегающие значения модуля радиус-вектора от 0 до R3. Дело в том, что именно эти поверхности плавно (с совпадающими касательными) переходят в трехмерную гиперсферу на поверхности пересечения с ней (на поверхности двумерной сферы), при условии равенства максимального радиуса этих роз радиусу трехмерной гиперсферы. Для такой геометрии существуют решения с равномерно (с одинаковой скоростью) растущим радиусом трехмерной гиперсферы, а также решения, позволяющие сделать выводы о существовании областей застоя (уплотнения) энергии, которые могут быть одним из видов темной материи.
     Простейшая формула такой одноугловой розы (одноугловая роза первого порядка и второй полноты): R=R3*|SIN(K*(угол тетта))|. Соответственно формула одноугловой розы первого порядка  и первой полноты: R=R3*|SIN(K*(угол тетта))/(SIN(K*(угол тетта))+ COS(K*(угол тетта))|. Соответственно формула одноугловой розы второго порядка  и первой полноты: R=R3*|(SIN(K*(угол тетта)))*(SIN(K*(угол тетта)))/(SIN(K*(угол тетта))+ COS(K*(угол тетта))|.Соответственно формула одноугловой розы первого порядка (третьей полноты)): R=R3*|SIN(K*(угол тетта))/((SIN(K*(угол тетта)))*(SIN(K*(угол тетта)))*(SIN(K*(угол тетта)))+ (COS(K*(угол тетта)))*(COS(K*(угол тетта)))*(COS(K*(угол тетта))))|. Далее по аналогии. Существуют и розы смешанной полноты - с разными степенями SIN и COS в знаменателе. Здесь угол тетта - это угол в полярных координатах между осью симметрии четырехмерного гиперполнотория, проходящей через точку S, и радиус вектором R описывающим соответствующую двумерную сферу на трехмерной поверхности розы. Для соответствующих участков розы, соответствующих верхнему и нижнему участку "Глобальной червоточины Вселенной"), соответственно выполняется: 0<угол тетта<(ПИ/2K); ПИ-(ПИ/2K)<угол тетта<(ПИ); K>1. Для нас в этом случае крайне интересно рассмотреть решения с K растущим в глобальном времени от 1 до до бесконечности: (1<K(T)<бесконечности). Тогда для формулы простейшей одноугловой розы первого порядка и второй полноты при K=1, мы получаем простейшую розу, которая сама является простейшим закрытым в точку (само-соприкасающимся) трехмерным гипертором, для которого выполняется условие (1/2)R1=R2=(1/2)R3 (где R1, R2 и (1/2)R3 - его главные образующие радиусы). (Для такой розы любое (для любых соответствующих углов омега) вертикальное сечение нашего трехмерного гипертора (являющегося трехмерной поверхностью нашего четырехмерного гиперполнотория) евклидовым пространством, содержащим ось симметрии нашего нашего трехмерного тора и ось ортогональную трехмерному пространству, в котором построена соответствующая двумерная тороидальная образующая поверхность, является закрытым в точку (само-соприкасающимся) двумерным тором, для которого выполняется равенство R2=(1/2)R3 (где R2 и (1/2)R3 - его два главных образующих радиуса). Этот случай как раз соответствует случаю, когда R1=R2 для обычного двумерного тора. Это будет являться повторением формы нашей двумерной образующей поверхности двумерной образующей поверхности нашего трехмерного тора при R1=R2.)) То есть для такая роза как раз и является начальной (при нашем рассмотрении) формой нашего трехмерного гипертора для некоторого начального с момента наступления стадии розы  момента глобального времени T(розы)=0.
     При дальнейшем развитии и росте параметра K(T) Вселенная становится глобально многосвязной в области "запрещенных" углов тетта, лежащих вне ранее указанных границ, (в случаях сохранения физического смысла для углов тетта, лежащих вне ранее указанных границ). Такая многосвязность может иметь многочисленные последствия, которые могут выражаться и обнаруживаться, например, в форме особых узлов темной материи в наблюдаемом трехмерном пространстве Вселенной, либо в форме появления особого гиперпространства в ненаблюдаемых (в наблюдаемом трехмерном пространстве Вселенной) областях дополнительной связности, имеющих место для углов тетта, лежащих вне ранее указанных границ.
     Такая многосвязность, в случае разрыва поверхностей дополнительных связностей (в области "запрещенных" углов тетта) с центром симметрии нашего трехмерного гипертора, может приводить к самопроизвольному замыканию разрывов и образованию "подпространственной пены" дополнительных связностей в виде трехмерных пузырьков дополнительного трехмерного пространства, первые (многие) из которых касаются трехмерной поверхности нашего трехмерного гипертора (то есть касающихся видимого пространства Вселенной), а вторые (другие) касаются первых пузырьков, и так далее. Эти пузырьки дополнительных связностей, обладающие большой энергией в силу большой кривизны их пространства, как раз и могут образовывать объекты, наблюдаемые в виде темной материи. А при достаточном их количестве их гипотетически можно использовать в качестве "гиперпространства фантастов" или кротовых нор физиков для путешествий со сверхсветовой скоростью.
      Подобная многосвязность, разрывы поверхностей  дополнительной связности и образование "подпространственной пены" могут многократно усиливаться в случае много-угловой розы. Простейшая формула такой двоугловой розы (двоугловая роза второго порядка (второй полноты)): R=R3*(|SIN(K*(угол тетта))|)*(|SIN(L*(угол омега))|). Здесь угол омега - как на рисунке - угол поворота вокруг оси симметрии нашего трехмерного гипертора.
      Для нас также важно, что с ростом T и соответственно с ростом K(T) максимальные векторы R соответствующие тетта=(ПИ/2K(T)) или тетта=ПИ-(ПИ/2K(T)) описывают трехмерную гиперсферу, если считать R3=const, или схематически (неполноценно) описывают расширяющуюся трехмерную гиперсферу, если считать, что R3(T) растет с ростом глобального времени T. При этом вполне разумно считать, что расширение Вселенной не имеет обратной динамики в односвязных областях. Но тогда указанное уравнение розы с таким допущением фактически описывает еще и сферическую деформацию нашего трехмерного гипертора по мере роста T и соответственно роста K(T) и роста R3(T).
     А для углов тетта, лежащих внутри ранее указанных границ, с ростом параметра K(T) "Глобальная червоточина Вселенной" сужается в соответствии с формулой для угла тетта. При этом средняя кривизна ее пространства убывает с ростом глобального времени T и соответственно с ростом K(T), в то время как ее кривизна в области ее сопряжения (границы)с усеченной трехмерной гиперсферой (в области углов тетта, определяемых формулой максимального R, а именно: K(T)*(угол тетта)= ПИ/2 (или =ПИ*(3/2)) наоборот быстро растет и начинает многократно (пропорционально K(T)) превышать кривизну трехмерной гиперсферы, которая с ростом T и соответственно с R3(T) наоборот убывает. Этот процесс приводит сначала к замедлению перетока энергии от "Глобальная червоточина Вселенной" к остальному наблюдаемому пространству Вселенной (имеющему форму усеченной трехмерной гиперсферы) вследствие увеличения кривизны пространства в области сопряжения двух указанных областей (двух указанных частей нашего трехмерного гипертора). А потом  этот процесс приводит к ускорению этого перетока энергии, вследствие достаточно сильно уменьшения кривизны каждой из сопрягаемых областей (двух указанных частей нашего трехмерного гипертора), при этом кривизна переходной области временно перестает быть сдерживающим фактором.  Когда "Глобальная червоточина Вселенной" становится критически узкой при достаточно больших T и K(T), то увеличившаяся кривизна переходной области снова начинает оказывать значительное влияние и переток энергии вследствие этих процессов снова замедляется вплоть до обрывов и прекращения этого перетока. Вероятно, что наша Вселенная не достигла стадии критически узкой "Глобальной червоточины Вселенной", но находится в стадии, когда  кривизна каждой из сопрягаемых областей (двух указанных частей нашего трехмерного гипертора) достаточно уменьшилась и кривизна переходной области временно перестала быть сдерживающим фактором для перетока энергии. Именно поэтому мы и наблюдаем ускорение перетока энергии из "Черной дыры Вселенной" в виде темной энергии и ускоренного расширения Вселенной.
   
     Поскольку получившийся таким образом четырехмерный гиперполноторий будет иметь центр симметрии в четырехмерном пространстве, то прямолинейный отрезок, соединяющий этот центр с любой точкой трехмерной поверхности этого гипертора (точкой трехмерного пространства Вселенной), необходимо (при такой геометрии) рассматривать как величину, содержащую локальное время в этой точке. Точнее локальное время в некоторой точке пространства Вселенной определяется длиной отрезка один конец которого является соответствующей точкой поверхности нашего трехмерного гипертора, а другой конец является точкой пересечения главной образующей двумерной поверхности нашего трехмерного гипертора с прямой, соединяющей его центр симметрии с указанной точкой его поверхности. Но, поскольку R1<<R2<<R3, то для определения локального времени в точках той части его поверхности, которая близка к трехмерной гиперсфере, можно использовать расстояние до его центра симметрии. Дело в том, что такой трехмерный гипертор постоянно раздувается в глобальном времени и радиус R3, определяющий глобальное время Вселенной, постоянно растет, что подтверждается наблюдаемым расширением Вселенной. Поэтому радиус R3 поверхности такого сферически деформированного гипертора и следует рассматривать как глобальное время или как некую пространственно-временную координату содержащую глобальное время. Если в рамках предлагаемой геометрии считать, что R3 это глобальное время, то поскольку R1 и R2 имет размерность расстояния (длины), то для соблюдения совпадения размерности R3 с размерностями R1 и R2, глобальное время необходимо ввести в привычной нам размерности времени. А именно для измерения времени в привычных нам размерностях вводим глобальное время T, определяемое формулой R3=T*C , где C является универсальной физической константой имеющей размерность скорости. При этом наиболее вероятно, что C является скоростью света в вакууме, или максимально близка к этой скорости, что подтверждается тем, что теоретическая скорость удаления от нас самых удаленных теоретически наблюдаемых звезд и галактик близка к скорости света в вакууме. (Согласно современным представлениям наиболее удаленный от нас наблюдаемый объект во Вселенной - галактика GN-z11 - расположен на расстоянии от нас около 13,4 миллиардов световых лет. Почти на таком же расстоянии расположены от нас и другие максимально удаленные от нас объекты по всем направлениям в пространстве. Возраст Вселенной оценивается астрофизиками в величину примерно 13,8 миллиардов лет. Следовательно, скорость удаления от нас этого объекта и других максимально удаленных объектов по другим направлениям в пространстве близка к скорости света.) Априори Земля не является центром Вселенной, следовательно, для любой точки (объекта) во Вселенной выполняется то же правило, что и для Земли, а именно: наиболее удаленные от такого объекта по всем направлениям другие видимые объекты во Вселенной находятся от него на расстоянии немного меньше, чем 13,8 миллиардов световых лет и удаляются от него со скоростью немного меньшей скорости света. Если исходить из величины возраста Вселенной в 13,8 миллиардов лет (это разумно, поскольку эта величина получена разными методами), то единственно возможный тип геометрии пространства, при котором такое возможно, это геометрия близкая к геометрии трехмерной гиперсферы, являющейся поверхностью четырехмерного гипершара. Такой тип геометрии включает в себя и предложенную мной геометрию трехмерной поверхности сферически деформированного трехмерного гипертора. Простейшее геометрическое построение подтверждает этот вывод. При такой геометрии в электромагнитных волнах (фотонах) мы можем наблюдать только одно полушарие, (а точнее гипер-сферический угол равный 2 радиана, то есть примерно 120 градусов, что меньше полушария с углом равным 180 градусов), трехмерной поверхности такого сферически деформированного объемного четырехмерного гиперполнотория. При этом мы, находясь в геометрическом центре такого полушария, всегда будем наблюдать, что одни и те же максимально удаленные видимые нами галактики и звезды будут всегда удаляться от нас со скоростями почти равными скорости света и не исчезают из вида, но при этом на горизонте Вселенной не будут появляться новые галактики и звезды, которых ранее было невозможно увидеть, что собственно пока и наблюдается.

     При этом каждый конкретный отрезок, соединяющий центр симметрии такого четырехмерного гиперполнотория с каждой конкретной точкой его трехмерной поверхности следует рассматривать как локальное время в этой точке. Поскольку реальная трехмерная поверхность такого четырехмерного гиперполнотория в реальной Вселенной представляет собой реальное трехмерное пространство Вселенной, то эта поверхность является реально неоднородной в смысле нарушения центральной сферической и осевой симметрии. Эта неоднородность вызвана во-первых, наличием видимой материи и связанных с нею гравитационных взаимодействий и связанных с ее движением релятивистских явлений, а во-вторых, эта неоднородность вызвана также иными собственными деформациями этой поверхности, которые наблюдаются в виде темной материи. Указанная неоднородность и приводит к тому, что для одного и того же глобального времени в различных точках реального трехмерного пространства Вселенной локальное время является неодинаковым. Каждая элементарная частица во Вселенной имеет свое собственное локальное время. Это выражается в частности в "парадоксе близнецов", а также в том, что атомы соединенные в молекулы и кристаллы не разлетаются, также и в том, что не разлетаются тела связанные гравитацией и иными взаимодействиями. С учетом перехода к привычным нам размерностям это локальное время определяем по формуле r3=t*C, где r3 является длиной отрезка, соединяющего центр симметрии (в четырехмерном пространстве) такого трехмерного гипертора с соответствующей конкретной точкой его поверхности, а t является локальным временем в этой точке.

     Такая геометрия гипер-тороидального пространства-времени напоминает геометрию гипер-шарового пространства-времени, где трехмерное пространство Вселенной является трехмерной гиперсферой, которая является трехмерной поверхностью четырехмерного гипершара. При этом единственный радиус этой трехмерной гиперсферы определяется формулой R=T*C, где T - глобальное время, а C - скорость света в вакууме или величина близкая к ней. Но в то же время предложенная мной геометрия является тороидальной геометрией, в которой анизотропность и глобальная неоднородность трехмерного пространства Вселенной заложены изначально, и этим она коренным образом отличается от изначально однородного и изотропного трехмерного пространства трехмерной гиперсферы.

     Если рассматривать традиционную теорию "Большого взрыва" в рамках однородного и изотропного (кроме направления времени) пространства-времени или же в рамках гипер-шарового пространства-времени, которое также является однородным и изотропным (кроме направления времени), то у точечного изначального источника энергии Вселенной нет никаких математических оснований к саморазвитию вследствие отсутствия "соотношений масштаба" в однородном и изотропном (кроме направления времени) пространстве-времени. Для такого точечного источника энергии трехмерное однородное и изотропное пространство, в том числе гипер-сферическое пространство, неотличимы от одномерного пространства, и даже единственно возможное в таких условиях соотношение масштаба R=T*C оказывается лишенным смысла, вследствие отсутствия масштабированной линейки для измерений. Именно поэтому я полагаю, что Большой взрыв и последующее появление и саморазвитие неоднородной и анизотропной Вселенной невозможны в однородном и изотропном (кроме направления времени) пространстве-времени. Кроме того, как я уже указывал ранее, в рамках гипер-шарового пространства-времени нам не удастся поместить глобальный гравитирующий объект (Черную дыру Вселенной) в геометрический центр этого гипер-шарового пространства-времени и, в то же время, остаться на поверхности этого гипер-шара, которая и будет при этом являться наблюдаемым трехмерным пространством. То есть такой глобальный объект неизбежно при этом оказывается вне наблюдаемого трехмерного пространства.

     Говоря о возможных геометриях реального пространства-времени Вселенной практически все ученые упускают вопрос о том, почему все основные физические константы и соответственно все физические законы одинаковы и неизменны во всей Вселенной во все времена.

     Полагаю что данный факт совершенно невозможно объяснить без признания еще одного основополагающего физического принципа - "принципа нелокальной связанности Вселенной". Речь здесь не только о том, что все взаимодействовавшие некогда элементарные частицы являются нелокально связанными хотя бы по импульсу, орбитальному моменту импульса и координатам, а иногда и по собственному моменту импульса. Я полагаю, что все точки или элементарные кирпичики реального пространства, а точнее пространства-времени, являясь реальными квантовыми объектами имеют нелокальную связь друг с другом (то есть мгновенное, совершаемое с бесконечной скоростью в глобальном времени взаимодействие друг с другом вне зависимости от расстояние между ними) через структуры глобального пространства-времени. И именно такое взаимодействие собственных квантов пространства-времени, совершаемое с бесконечной скоростью, и обеспечивает одинаковость и неизменность всех основных физических констант и соответственно всех физических законов. В том числе оно обеспечивает известную каждому физику нелокальную связанность взаимодействовавших элементарных частиц.
При этом сами величины самих основных физических констант определятся так называемыми "соотношениями масштаба" к которым относится в первую очередь геометрия глобального пространства времени, а именно: степень и форма сферической деформации глобального пространства-времени, изначальное несовпадение и соотношение главных геометрических радиусов R1, R2 и R3, соотношение скорости расширения Вселенной, определяемой скоростью увеличения радиуса R3, и линейных скоростей вращения глобального пространства, соотношение угловых скоростей вращения глобального пространства вдоль главных геометрических окружностей вышеуказанного глобального гипертора, соотношение энергий таких вращений, соотношения указанных энергий и иных глобальных энергий, а также всей глобальной массы Вселенной и энергии расширения Вселенной, а также иные возможные соотношения глобальных параметров глобального пространства-времени . Полагаю, что наблюдаемая неизменность основных физических констант объясняется неизменностью или относительно высокой стабильностью вышеуказанных "соотношений масштаба".

   Хотя к соотношениям масштаба мы отнесли и вышеупомянутую формулу R3=T*C, однако полагаю, что универсальная константа C, совпадающая, по-видимому, со скоростью света в вакууме, сама определяется иными, а именно базовыми соотношениями масштаба, например соотношением глобальной инерционной массы и глобальной энергии Вселенной, определяемой формулой E=M*C*С.