Парадокс аксиомы связей в СТО

   Пусть на рельсах стоит вагон (стержень). Пусть к нему подъезжает точечный паровоз и в результате неупругого удара вагон (стержень) приобретает скорость V. Пусть граница  гипотетического универсального  взаимодействие жесткости распространяется по стержню со скоростью света. Т.е. скорости точек стержня между паровозом и бегущей по стержню границей будут равны V. А скорости точек между границей и покоящимся концом будут равны нулю. Собственно говоря , это описание и есть определение релятивистки жесткого стержня школьными средствами. Физическое описание максимально возможной жесткости.
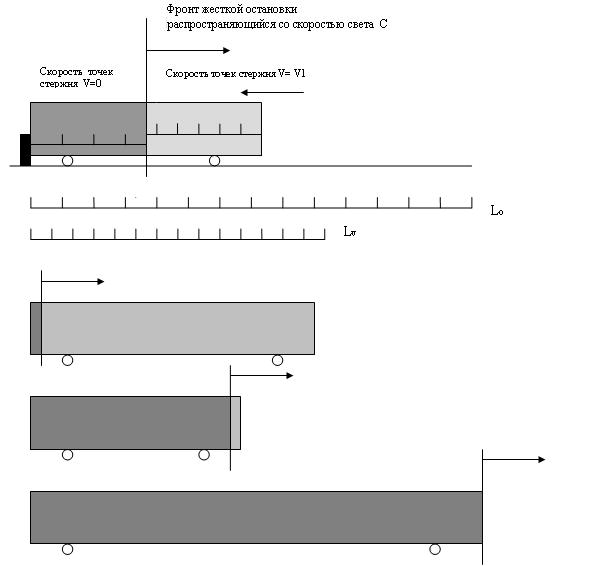
   Теперь рассмотрим остановку вагона, которая происходит в том же порядке. Но вызывает большее беспокойство. Т.к. именно в этом случае, очевидно, что если разбить стержень на отрезки и промаркировать их, то их количество вместе с распространением границы взаимодействия будет уменьшаться вместе с длинной стержня. После достижения  границей  взаимодействия движущегося конца, скорость последнего изменится. Длинна стержня со скоростью света увеличится до длинны покоя.
  При этом количество и длины промаркированных отрезков увеличатся до количества и длин отрезков в состоянии покоя.
   Аналогичная ситуация наблюдается и в первом случае, хотя и менее очевидна.

  Т.о. при импульсном изменении скорости  жесткого в вышеприведенном смысле стержня часть его длинны и часть его точек (отрезок) в течение отрезка времени не равном нулю в  ИСО не наблюдается.

В случае для импульса действующего на растяжение абсолютно жесткого стержня придется при таком подходе признать что часть длинны вытягивается из небыти и даже в состоянии покоя в ИСО наблюдаются не все точки стержня.

- Вовочка, какое время года сейчас?
- Лето!
- Но,Вовочка, посмотри! Снег лежит.Холодно.
- Вот такое у нас лето, Маривановна!


© Copyright: Эдя Псковский, 2010
Свидетельство о публикации №210031900312

Уточним. Как только конец стержня тормозится, так стержень разбивается на две области. Область где точки остановлены и эта область распространяется со скоростью света и область где они еще движутся. Минимальную длину стержень имеет когда движущийся конец смыкается с фронтом распространения неподвижных точек.
Если считать стержень цепью связанных материальных точек (если), то потери суммарной массы покоя не произойдет. Просто на фронте торможения линейная плотность точек возрастает до бесконечности и нарушается требование абсолютной жесткости. И в конечном итоге он от минимальной длины  распрямится со скоростью света до  длинны покоя.

Максимально просто парадокс аксиомы связей проявляется в случае, если мы на Земле начинаем с максимальной скоростью тянуть за конец невесомого АБСОЛЮТНО ЖЕСТКОГО троса, другой конец которого закреплён на Альфе Центавра. И за 4 года можно вытянуть 4 световых года троса, хотя его конец еще будет находиться на Аьфе Центавра. Т.е. динамическая длина абсолютно жесткого троса может быть вдвое большей его длины , когда концы троса покоятся неограниченно долгое время.