Мягкие математические модели роста популяций

(Статья опубликована в сборнике научных статей докторантов и аспирантов Московского государственного университета леса, 2002. С.19)

Основная модель популяционного роста, используемая в экологических исследованиях, — это модель Ферхюльста, или логистическое уравнение:

dN/dt = rN (1–N/K),           (1),

где N(t) — численность популяции в момент времени t, r — наибольшая удельная скорость роста, K — емкость среды, N/K — доля доступных ресурсов, потребляемая популяцией размера N, а множитель (1–N/K) описывает долю неиспользованных ресурсов. На этой модели основаны уравнения конкуренции Лотки–Вольтерры, принцип конкурентного исключения Гаузе и, в конечном счете, понятие экологической ниши, т.е. многие базовые понятия синэкологии [1].

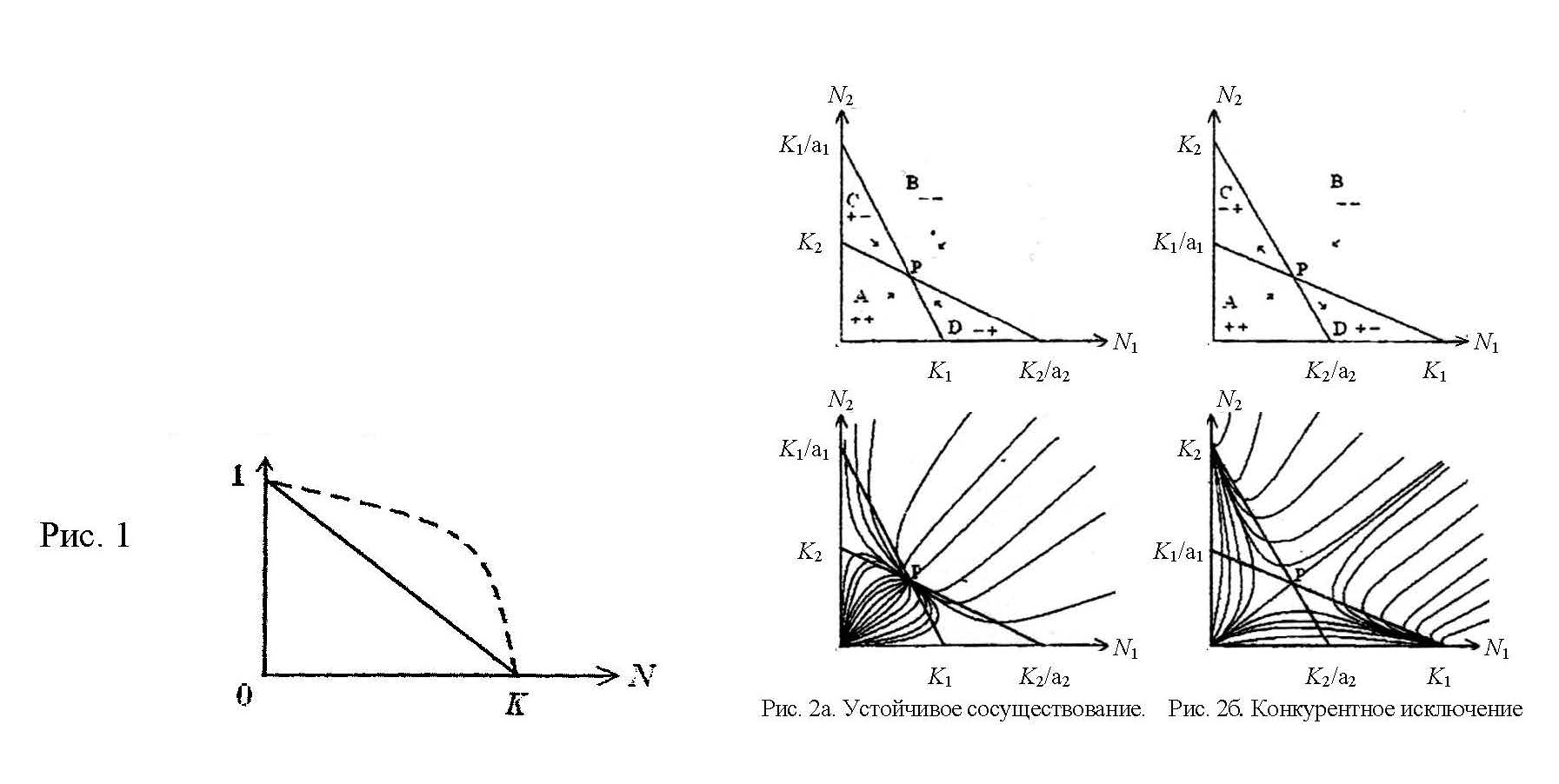
Полезность этой модели, ее прекрасное согласие с огромным количеством натурных наблюдений и экспериментов нуждаются, тем не менее, в объяснении. По Ферхюльсту, благодаря стоящему в правой части уравнения (1) множителю (1–N/K) создается эффект торможения роста популяции — вследствие исчерпания растущей популяцией лимитирующих ресурсов среды обитания или же накопления вредных отбросов (самоотравления). Однако и в том и в другом случае нет оснований приписывать множителю при r N линейный характер. Реалистичнее полагать, что при низкой плотности популяции эффекты насыщения будут едва заметны, и, напротив, по мере приближения численности популяции к критической они будут нарастать очень резко, т.е. множитель при r N будет вести себя, как изображено на пунктирной кривой рис. 1.

Почему же, несмотря на явную нереалистичность исходного допущения о линейной зависимости насыщения от численности популяции, важнейший вывод из логистической модели популяционного роста — принцип Гаузе — так хорошо согласуется с реальностью? Все дело в том, что этот вывод носит не количественный, а качественный характер. Это финалистский принцип, описывающий конечный результат конкуренции: будет ли сосуществование двух конкурирующих видов устойчивым или один из них в конце концов вытеснит другой. Динамика борьбы за существование им не описывается, да она и не важна для прогноза, носящего столь общий характер.

Угол наклона пунктирной кривой на рис. 1 в каждой точке определяется выбором масштаба по оси абсцисс, и, локально изменяя этот масштаб, мы всегда можем сделать любую строго монотонно убывающую гладкую кривую прямой. Подобное неравномерное сжатие-растяжение рисунка по направлению одной из осей называется в физике калибровочным преобразованием, а в математике — диффеоморфизмом. В качественной теории устойчивости особенности векторного поля фазовых скоростей системы всегда рассматриваются с точностью до диффеоморфизма.

В самом деле, в прогнозе развития таких систем нас обычно интересует не геометрия отдельных траекторий, а топология совокупности всех траекторий: будут ли они замкнутыми (колебательный режим) или разомкнутыми, сходиться к одной точке или уходить на бесконечность, и так далее. При гладкой (непрерывно дифференцируемой) замене переменных эти топологические характеристики не меняются, а значит, все выводы, основанные только на таких характеристиках, остаются в силе [2].

Рассмотрим, например, доказательство принципа конкурентного исключения. Для этого выпишем уравнения типа (1) для двух видов, обитающих в одной местности и претендующих на одни и те же ресурсы, причем для каждого вида доля необходимых ему ресурсов, потребляемых ими вместе, считается пропорциональной численностям обоих видов:

dN1/dt = r1N1 [1 – (N1 + a1N2)/K1],              (2)
dN2/dt = r2N2 [1 – (N2 + a2N1)/K2].              (3)

Здесь взят наиболее общий случай: ёмкости среды для каждого вида K1 и K2, максимальные скорости размножения (мальтузианские коэффициенты) r1 и r2, а также коэффициенты а1 и а2, описывающие относительные экологические потребности каждого вида, могут быть какими угодно, как совпадающими, так и различными.

Хотя система (2)–(3) задаётся шестью параметрами, ниже мы увидим, что качественные особенности её фазового портрета (всей совокупности траекторий в фазовом пространстве) определяется только четырьмя из них: K1, K2, а1 и а2.

Мальтузианские коэффициенты r1 и r2 влияют лишь на углы наклона траекторий в фазовом пространстве (меняющиеся, как и на рис.1, в зависимости от выбора масштаба по осям), но не на взаимное расположение этих траекторий — оно от них совершенно не зависит. Ведь никакое изменение масштаба не может сделать убывающую функцию возрастающей, и наоборот. Функции характеризуются своими экстремумами — точками, где их производные обращаются в нуль. А нули производных dN1/dt и dN2/dt достигаются либо на соответствующих координатных осях (dNi/dt = 0 при Ni = 0, i = 1, 2), либо там, где обращаются в нуль множители в квадратных скобках в правых частях уравнений (2)–(3). Итак, dN1/dt =0 на прямой N1 + a1N2 = K1 и на оси N1 = 0, а dN2/dt = 0 на прямой N2 + a2N1 = K2 и на оси N2 = 0. Внутри областей фазовой плоскости {N1, N2}, ограниченных указанными прямыми, составляющие вектора фазовой скорости остаются знакопостоянными. Этой информации достаточно для качественного описания поведения интегральных кривых на фазовой плоскости.

Так, на рис. 2а и на рис. 2б в области А численности обоих видов растут (сигнатура + + ), и поле скоростей направлено вверх и вправо, как показывают стрелки, а в области В численности обоих видов убывают (сигнатура – – ), т.е. поле скоростей в этой области везде направлено вниз и влево. Но в областях С и D указанные стрелками направления и сигнатуры для случаев 2а и 2б прямо противоположны: для устойчивого сосуществования (2а) траектории в этих областях сходятся к стационарной точке Р, а для случая конкурентного исключения (2б) траектории в этих областях удаляются от точки Р. Линии, на которых численность одного из видов достигает экстремального значения и соответствующая компонента фазовой скорости обращается в нуль, называются изоклинами нулевого роста; на них сигнатура меняется, а точка их пересечения Р — это стационарное состояние, устойчивое или неустойчивое, в котором обе компоненты фазовой скорости равны нулю. Ясно, что указанные свойства фазового портрета не зависят от выбора масштаба по осям, и различие между случаями 2а и 2б не количественное, а качественное. В первом случае K1 < K2/а2 и K2 < K1/a1, а во втором случае K1 > K2/a2 и K2 > K1/а1. (Два оставшиеся случая, когда K1 < K2/a2 и K2 > K1/а1 , а также когда K1 > K2/а2 и K2 < K1/a1, анализируются аналогично и тривиальны, так как при этом изоклины не пересекаются, так что стационарной точки просто нет — сосуществование длится недолго).

Как и в рассмотренном выше примере нелинейной зависимости эффектов торможения от численности популяции, доказательство принципа конкурентного исключения без труда обобщается на нелинейные зависимости скорости роста популяций двух видов от их численностей, если фазовые портреты этих нелинейных систем топологически подобны показанным на рис. 2 (т.е. изоклины нулевого роста, теперь уже криволинейные, пересекаются лишь в одной точке). Вот почему принцип конкурентного исключения в сущности не зависит от предположения о линейности этих зависимостей.

В этом и состоит принципиальное различие описания борьбы за существование у Мальтуса и Дарвина, с одной стороны, и у Лотки–Вольтерры–Гаузе, с другой. В первом способе учитываются только мальтузианские коэффициенты: именно они описывают дарвиновскую приспособленность, тогда как экологические характеристики полностью игнорируются. Во втором способе, напротив, исход конкуренции определяется экологическими особенностями конкурирующих видов и не зависит от соотношения скоростей их размножения в одинаковых природных условиях.

Этот пример иллюстрирует более общий принцип, относящийся к выбору математических моделей, описывающих установившиеся (стационарные) режимы биологических систем. Как правило, такие режимы обладают гомеостатическими свойствами, т.е. устойчивостью к «малому шевелению» описывающих их кривых, т.е. к варьированию параметров этих кривых. Ведь природная среда никогда не бывает строго однородной в пространстве и времени, в ней всегда присутствуют возмущения, и саморегуляция природных систем с необходимостью должна обеспечивать устойчивость к возмущениям, иначе эти системы просто не могли бы существовать сколько-нибудь долго. Устойчивость природных систем не только эмпирический факт, она логически необходима для их существования, а потому все математические модели для описания таких систем, претендующие на реалистичность, должны обеспечивать эту устойчивость. В математике системы, качественные особенности которых сохраняются при малых изменениях параметров, называются структурно устойчивыми, или грубыми (мягкими). Отсюда вытекает необходимость применения в математическом моделировании устойчивого развития природных систем только мягких моделей.

Однако и в природных системах  может возникать хаос, и тогда  их поведение становится непредсказуемым. Но в этом случае количественный прогноз невозможен в принципе, и роль математического моделирования сводится к воспроизведению этого хаоса и анализу критических значений параметров, при которых устойчивое поведение сменяется хаотическим и наоборот (см., например, [3]).

Аналогичные соображения объясняют успешность применения в биометрии линейных статистических методов — линейного дискриминантного анализа и факторного анализа. Неоднократно указывалось, что эти методы не имеют строгого математического обоснования, но они широко и успешно используются в самых разных разделах наук о природе. Здесь также статистическая устойчивость результатов наблюдений задним числом оправдывает применение линейного приближения: если изучаемые различия между естественными совокупностями реальны и сами эти совокупности также «естественны», то эти различия должны сохраняться при гладком калибровочном преобразовании исходного пространства признаков в пространство, в котором метрику можно считать евклидовой. Произвол в выборе метрики, независимость качественного поведения системы от этого выбора — это и есть основное свойство мягких моделей.

ЛИТЕРАТУРА

1.Вольтерра В. Математическая теория борьбы за существование. — М.:Наука, 1976. С.285.
2.Арнольд В.И. «Жесткие» и «мягкие» математические модели. — Доклад на семинаре «Аналитика в государственных учреждениях» при Администрации Президента Российской Федерации 25.09.97.
3.Чудов С.В., Чудова Н.Г. Колебания численности популяций и хаос в динамических системах: Сборник научных статей докторантов и аспирантов МГУЛа. — М.: МГУЛ, 1999. С.58.