Обходимся без функции Ламберта. Ч 1

Конечно, я всегда стремлюсь находить общие формулы, чтобы подставить конкретные параметры и выявить окончательное решение. Но иногда приходится идти по самому кратчайшему пути и проверять правильность общей формулы, найденной кем-то из математиков. Вот пример по ссылке:
https://www.youtube.com/watch?v=RFhcvmW5ttI
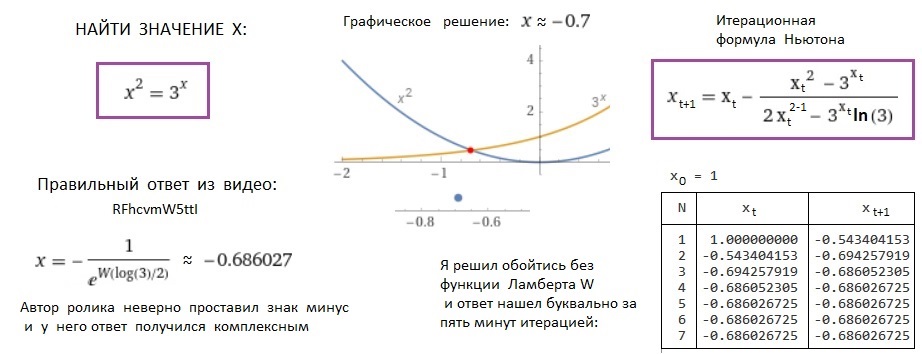
Автор долго вымучивал решение и оно оказалось ошибочным. Помогли мне приближенные методы. Во-первых, графический. В иллюстрации это наглядно показано и четко видно, что имеется единственный корень, который приблизительно равен -0.7. Ответ же в упомянутом видео оказался даже не вещественным, а комплексным. Где тогда ошибка? В графиках или у преподавателя? В качестве арбитра был выбран прекрасный метод итерации Ньютона. Итерационная формула приведена в иллюстрации. За буквально минуты написал программу:

rem Обходимся без функции Ламберта W(z)
x0=1
print " x0 = ";:print x0
print "---------------------------------"
print "  N       x0             x "
print "---------------------------------"
for i=1 to 7
x=x0-(x0^2-3^(x0))/(2*x0^(2-1)-3^(x0)*log(3))
print i using "###" ,x0 using "###.#########";
print x using "###.#########"
x0=x
next i

Решение в виде таблицы тоже привел. Оказалось, что x = -0.686026725  и это вполне корреспондируется с графиками. У преподавателя нашел ошибку - он знак минуса не там проставил. Ошибка, конечно, маленькая, но весьма существенная для математики.
Что же касается программы, то достаточно было задать всего семь циклов итерации, чтобы с большой точностью найти значение "x". Причем начальное значение этого параметра можно задать хоть положительное, хоть отрицательное. Все равно ответ сходится к значению, которое я выше привел. Этот же результат дал и Вольфрам Альфа.


7 июля 2023 г.