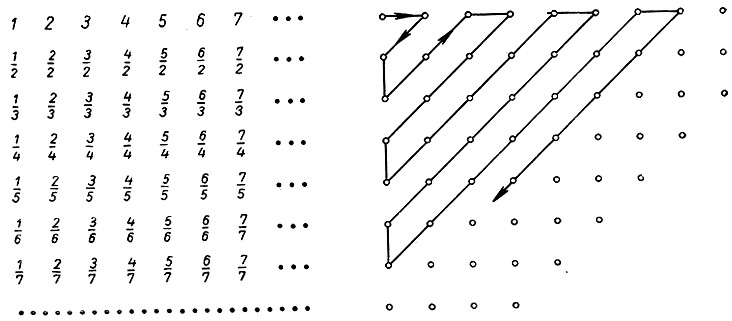
Свёртка Кантора для множеств чисел

Великий математик Георг Кантор, основатель теории множеств
https://ru.wikipedia.org/wiki/Кантор,_Георг
В 1874 году опубликовал в «Журнале Крелле» статью, в которой ввёл понятие мощности множества и показал, что рациональных чисел столько же, сколько натуральных, а вещественных гораздо больше.
Для этого он предложил диагональный метод – алгоритм свёртки (приведение во взаимное и однозначное соответствие) множества рациональных чисел Q https://ru.wikipedia.org/wiki/Рациональное_число
к множеству целых чисел Z https://ru.wikipedia.org/wiki/Целое_число
 

На мой взгляд, суть этого фундаментального открытия – операции преобразования множеств (таблиц в строки, матриц в вектора, плоскостей и поверхностей в линию) оказалась недооценённой и математики пошли неверной дорогой; что привело многих в заблуждения о счётности и мощности множеств.
https://ru.wikipedia.org/wiki/Счётное_множество
https://ru.wikipedia.org/wiki/Мощность_множества

Теперь я постараюсь пояснить своё мнение.
Существует заблуждение о том, что если иррациональное число
https://ru.wikipedia.org/wiki/Иррациональное_число
не является рациональным, то оно несчётно. (Это подмена понятий) То есть навязывается мнение о том, что такие числа как корень из 2 выпадают из последовательного подсчёта.

В действительности, как я считаю, такие числа тоже можно посчитать, приводя их во взаимное и однозначное соответствие рациональным числам, а следовательно, и к целым, благодаря применению операции диагональной свёртки Кантора к паре X^Y, где X, Y – рациональные числа.

Для этого сформируем таблицу, откладывая по горизонтали основания степени X, а по вертикали – показатели степени Y; где X и Y – счётные множества рациональных чисел. Тогда каждая пара X^Y войдёт в новое счётное множество. В том числе корень из 2.

Аналогичным образом можно посчитать комплексные числа a + i*b. Это уже будет 3 применение свёртки Кантора. Однако, возможна такая свёртка только для целых или рациональных чисел a и b.

Теперь несколько замечаний, выводов и предложений.

Мне неизвестно о вхождении констант пи и е в приведённые перечисления чисел. Это открытый вопрос. Всё зависит от выбора алгоритма свёртки.
В случае степенной показательной свёртки X^Y возможно дублирование чисел. Этот вопрос требует исследования. Видимо требуется наложить ограничения.

Предлагаю расширить и исследовать свёртку Кантора как фундаментальную операцию отображения множеств.

Предлагаю пересмотреть понятие мощности множеств. А именно:
Мощность 0 применять по отношению ограниченных, конечных множеств.
Мощность 1 – для целых чисел, по аналогии с рядами, векторами и размерностью пространства.
Мощность 2 – для рациональных чисел и целых комплексных чисел.
Мощность 3 или 4 – для радикалов рациональных чисел (иррациональных?), и комплексных рациональных.
ИТД ИТП.
Другими словами – мощность множества – это сколько раз применялась свёртка Кантора, мерность пространства, ранг тензора.

И ещё открыт вопрос о применении свёртки Кантора к кватернионам и октанионам.