Основные законы механики и внутренние силы

           Аннотация: преобразование прямолинейного движения во вращательное или колебательное под действием внутренних сил взаимодействующих тел
порождает появление динамических внутренних сил, влияющих на положение центра масс замкнутой системы тел.   

           Рассмотрим основные теоремы классической механики и их условия применения.
           Теорема о движении центра масс [1, с.44-45]: центр масс механической системы движется как материальная точка, масса которой равна массе всей
 системы и на которую действует сила, равная геометрической сумме всех внешних сил, приложенных к точкам системы.
           M(dvC /dt) = Fe                (1.1)
          Теорема об изменении количества движения [1, с.49-50]: производная по времени от количества движения механической системы равна главному вектору всех внешних сил.
          d(mv)/dt = Fe                (1.2)
          Следует отметить, что теорема об изменении количества движения тождественна теореме о движении центра масс [1, с.54] и, кроме того, теорема о
 движении центра масс [3, с.290] является следствием теоремы об изменении количества движения.
           Следствием из теоремы об изменении количества движения системы является закон сохранения количества движения [1, с.50]: если главный вектор
 внешних сил равен нулю, то количество движения системы остаётся постоянным.
            mv = const                (1.3)
            Следует отметить, что по свойству внутренних сил [1, с.43] сумма внутренних сил равна нулю Fe = 0.
           Теорема об изменении кинетической энергии системы тел [1, с.78-80]: изменение кинетической энергии при переходе механической системы из одного положения в другое равно сумме полных работ всех внешних и внутренних сил.
             Т2 - Т1 = Аe + Аi                (1.4)
          Равенство (1.4) верно для прямолинейного, вращательного и сложного движения. Главное отличие теоремы об изменении кинетической энергии от
вышеприведённых заключается в том, что кинетическая энергия зависит от работы внутренних сил.
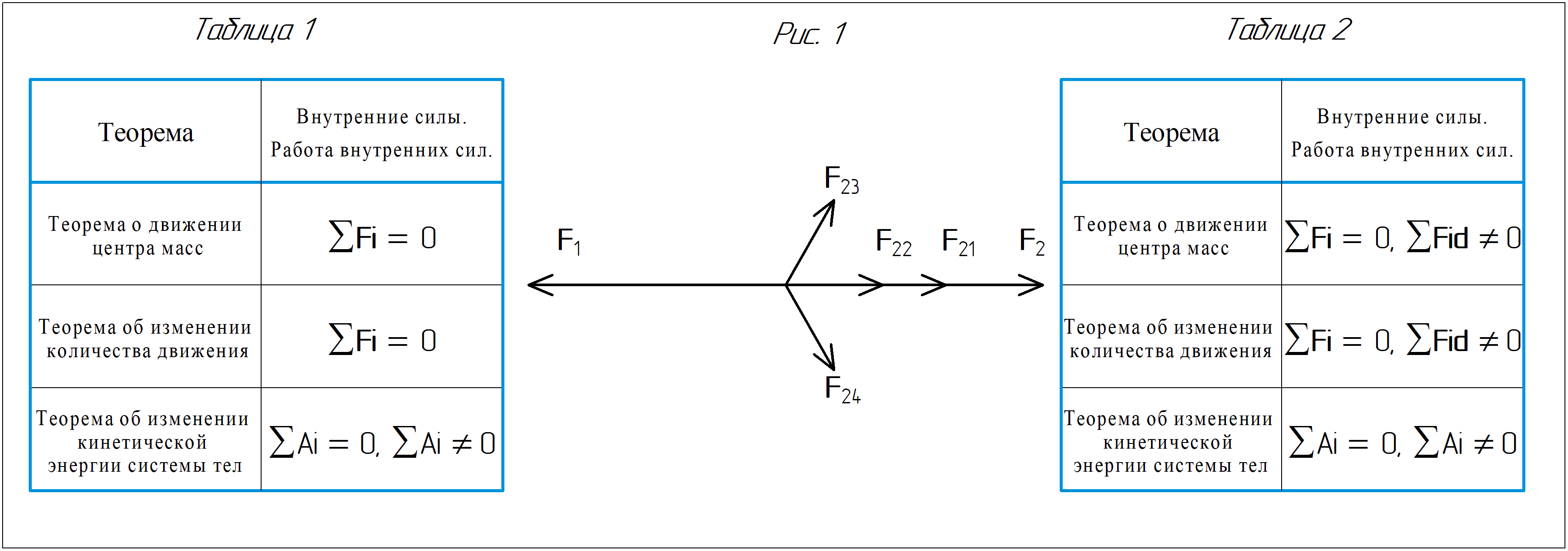
          Составим таблицу 1 основных теорем механики для внутренних сил и работ внутренних сил замкнутой (Fe = 0, Аe = 0) системы тел и рассмотрим выполнение закона сохранения импульса (количества движения) в этой системе.

          1 Работа внутренних сил (Аi =0) равна нулю, направления векторов сил параллельны.
         Пусть система состоит из двух движущихся прямолинейно навстречу друг другу тел массой m1 и m2 со скоростью v1 и v2 соответственно. После абсолютно
упругого взаимодействия тела приобретают в первом случае прямолинейное движение со скоростями v3 и v4, а во втором случае сложное движение:
прямолинейное движение со скоростями v5 и v6 и вращательное с угловыми скоростями w1 и w2 соответственно. Отметим, что при абсолютно упругом взаимодействии работа внутренних сил (Аi = 0) равна нулю.
          Запишем закон сохранения импульса и кинетическую энергию до и после взаимодействия для первого случая
           m1v1 + m1v2 = m1v3 + m2v4 = C1                (1.5) 
           m1((v1)^2)/2 + m2((v2)^2)/2 = m1((v3)^2)/2 + m2((v4)^2)/2.  (1.6) 
Легко доказать, что система уравнений из формул (1.5) и (1.6) имеет решение, то есть закон сохранения импульса выполняется.
Запишем кинетическую энергию для второго случая
          m1((v1)^2)/2 + m2((v2)^2)/2 = m1((v5)^2)/2 +
          m2((v6)^2)/2 + J1((w1)^2)/2 + J2((w2)^2)/2.             (1.7) 
При ближайшем рассмотрении формул (1.6) и (1.7), очевидно, что кинетическая энергия прямолинейного движения после взаимодействия во втором случае меньше и величина скорости тоже меньше, то есть
          v5 < v3                (1.8) 
и
          v6 < v4.                (1.9) 
Запишем отдельно сумму импульсов для второго случая до взаимодействия, из формулы (1.5)
          m1v1 + m2v2 = C1.                (1.10)
Теперь запишем сумму импульсов прямолинейного движения для второго и первого случая после взаимодействия
          m1v5 + m2v6 = C2                (1.11) 
          m1v3 + m2v4 = C1.                (1.12) 
Учитывая неравенства (1.8) и (1.9), очевидно, что из уравнений (1.11) и (1.12)
           C2 < C1.                (1.13) 
Значит во втором случае сумма импульсов прямолинейного движения до взаимодействия и после взаимодействия не равны друг другу
          |m1v5 + m2v6| < |m1v1 + m2v2|.                (1.14) 
          Таким образом, закон сохранения импульса для второго случая сложного движения с прямолинейным и вращательным движением, в данном случае, при работе внутренних сил равной нулю не выполняется.
         Следовательно, при сложном движении центр масс замкнутой системы тел меняет своё положение

2 Работа внутренних сил Аi не равна нулю, направления векторов сил параллельны.
         Пусть система состоит из двух тел массой m1 и m2, в начальный момент времени находящихся в покое. После взаимодействия тела приобретают в первом
случае прямолинейное движение со скоростями v1 и v2, а во втором случае сложное движение: прямолинейное движение со скоростью v3 и вращательное с
угловой скоростью w1 для первого тела и той же, как в первом случае, прямолинейной скоростью v2 для второго тела.
          Запишем закон сохранения импульса и кинетическую энергию после взаимодействия для первого случая
          m1v1 + m2v2 = 0                (1.15) 
          m1((v1)^2)/2 + m2((v2)^2)/2 = А1+А2.                (1.16) 
Легко доказать, что система уравнений из формул (1.15) и (1.16) имеет решение, то есть закон сохранения импульса выполняется.
Запишем кинетическую энергию для второго случая
           m1((v3)^2)/2 + J1((w1)^2)/2 + m2((v2)^)/2 =  А1 +А2           (1.17) 
При ближайшем рассмотрении формул (1.16) и (1.17), очевидно, что кинетическая энергия прямолинейного движения тела массой m1 после
взаимодействия во втором случае меньше, а значит и скорость тоже меньше, то есть
            v3 < v1.                (1.18) 
Запишем закон сохранения импульса прямолинейного движения для второго случая после взаимодействия
          m1v3 + m2v2 = 0.                (1.19)
Из формул (1.15) и (1.19) найдём скорости v1 и v3 получим
          v1 = -m2v2 /m1                (1.20) 
          v3 = -m2v2 / m1.                (1.21)
Из формул (1.20) и (1.21) вытекает, что v3 = v1, но согласно доказанному по формуле (1.18) v3 < v1. Получили противоречие. Следовательно, закон
сохранения импульса не выполняется и в этом случае, то есть при работе внутренних сил не равной нулю и сложном движении центр масс замкнутой
системы тел, находящийся в начальный момент времени в покое, меняет своё положение.
           Таким образом, при взаимодействии тел со сложным движением центр масс замкнутой системы меняет своё положение.
          Энергия вращательного движения может переходить в энергию поступательного движения и наоборот [5, с.424-428], доказано на примере взаимодействия двух стержней с шарами на концах.  Кроме того, приведено
математическое доказательство и экспериментальное подтверждение [4, с.28-41] движения центра масс под действием внутренних сил на примере полого и сплошного цилиндров одинакового внешнего диаметра и равной массы при
движении по наклонной поверхности. А также приведено математическое доказательство с выводом уравнений движения центра масс [6, с.197-202] на
примере двух грузов, вращающихся синхронно навстречу друг другу, то есть импульс центра масс системы может быть изменён путём изменения
внутреннего вращательного импульса или внутреннего поступательного импульса. Существует математическое доказательство [2, с.139-142] движения
центра масс системы тел под действием внутренних сил для замкнутой системы с колечками на стержне, взаимодействующих с ускорением под действием
пружин, и выведено уравнение движения центра масс под действием внутренних сил.
           Тогда, например, при взаимодействии двух тел можно сделать вывод, что возникают симметричные (рис 1), зеркально направленные равные силы F23 и F24
вызывающие вращение, но при этом сумма всех внутренних сил равна нулю. То есть, согласно 3-му закону Ньютона силы, действующие при взаимодействии
двух тел равны и противоположно направлены F1 = -F2. Так как второе тело начинает вращаться и двигаться поступательно, тогда вектор
            F2 = F21 + F22,                (1.22)
где F21 – вектор силы поступательного движения,
       F22 – вектор силы вращательного движения.
Вектор силы вращательного движения равен по правилу параллелограмма
           F22 = F23 + F24.                (1.23)
          Следовательно, в замкнутой системе тел при их взаимодействии со сложным движением возникают внутренние силы оказывающие разное влияние
 на характер движения тел, что позволяет выделить силы, вызывающие вращение и выделить силы – динамические внутренние силы, которые обеспечивают
поступательное движение центра масс и, которые должны фигурировать в теореме об изменении количества движения, как другой вид
внутренних сил, подчиняющихся в сумме с другими внутренними силами свойству внутренних сил равных нулю в замкнутой системе тел, но
оказывающих влияние на прямолинейное движение центра масс одновременно с силами, вызывающих вращение тел в системе.
          Динамической внутренней силой в данном примере является разность между силой взаимодействия 1-го тела F1 и силы взаимодействия поступательного движения 2-го тела F21
          Fid = F1 - F21                (1.24)
           Таким образом, теорема об изменении количества движения должна
формулироваться следующим образом: производная по времени от количества
движения механической системы равна главному вектору всех внешних
и внутренних динамических сил.
         d(mv)/dt = Fe + Fid                (1.25)
          Соответственно изменится и закон сохранения количества движения: если главный вектор внешних и внутренних динамических сил равен нулю, то количество движения системы остаётся постоянным.
          mv = const                (1.26)
          Теорема о движении центра масс так же изменится: центр масс механической системы движется как материальная точка, масса которой равна массе всей системы и на которую действует сила, равна геометрической
сумме всех внешних и внутренних динамических сил, приложенных к точкам системы.
          M(dvC /dt) = Fe + Fid                (1.27)
          Теорема об изменении кинетической энергии системы тел не меняется, так как в ней уже присутствует работа всех внутренних сил.
          Таким образом, таблица 1 основных теорем механики, замкнутой (Fe = 0, Аe = 0) системы тел, изменится для внутренних сил и будет иметь вид, который отображён в таблице 2. 

           Вывод: внутренние динамические силы, возникающие при преобразовании прямолинейного движения взаимодействующих тел во вращательное или колебательное, вызывают поступательное движение центра масс замкнутой системы тел.

                СПИСОК ЛИТЕРАТУРЫ:

1. Андронов В.В. Теоретическая механика. 20 лекций. Ч.2. Динамика: Учебное пособие для студентов очного и заочного обучения. Спец. 260100 и 260200. 2-е изд., доп. и испр. – М.: МГУЛ, 2003, – 128 с.
2. Геронимус Я. Л. Теоретическая механика (очерки об основных положениях): Главная редакция физико-математической литературы изд-ва «Наука», 1973г., 512с.)
3. Добронравов В.В., Никитин Н.Н. Курс теоретической механики: Учебник для машиностроит. спец. вузов. — 4-е изд., перераб. и доп. —М.: Высш. школа», 1983, – 575 с., ил.
4. Турышев М.В., О движении замкнутых систем, или при каких условиях не выполняется закон сохранения импульса., «Естественные и технические науки»,№3(29), 2007, ISSN 1684-2626.
5. Хайкин С.Э. Физические основы механики, М.: Наука, 1971, 752с.
6. Шипов Г.И. Теория физического вакуума. Теория эксперименты и технологии. 2-е изд., – М.:Наука, 1996, 456с.